 Problem B. 4435. (March 2012)
Problem B. 4435. (March 2012)
B. 4435. T is the foot of the altitude drawn from vertex A of an acute-angled triangle ABC. The midpoint of side BC is F. The centres of the squares drawn over the sides AB and AC on the outside are K and L, respectively. Prove that KTFL is a cyclic quadrilateral.
(Suggested by Sz. Miklós, Herceghalom)
(4 pont)
Deadline expired on April 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Kicsit pontosabban azt igazoljuk, hogy a \(\displaystyle K\), \(\displaystyle T\), \(\displaystyle F\), \(\displaystyle L\) pontok egy körön vannak. Ha \(\displaystyle AB=AC\), akkor \(\displaystyle F\) és \(\displaystyle T\) egybeesik, az állítás pedig nyilvánvaló. Szimmetria okok miatt feltehetjük, hogy \(\displaystyle AB<AC\), azzal a megjegyzéssel, hogy az \(\displaystyle AC>AB\) esetben a \(\displaystyle KFTL\) négyszög lesz húrnégyszög.
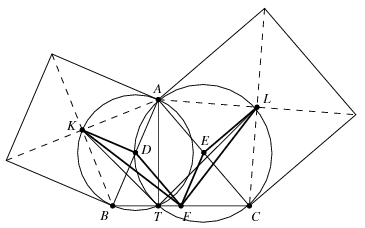
Mivel az \(\displaystyle AKB\) és az \(\displaystyle ATB\) szög is derékszög, az \(\displaystyle AKBT\) négyszög húrnégyszög, és így \(\displaystyle ATK\angle=ABK\angle=45^\circ\). Hasonlóképpen kapjuk, hogy \(\displaystyle ATL\angle=ACL\angle=45^\circ\), vagyis \(\displaystyle KTL\angle=ATK\angle+ATL\angle=90^\circ\). Már csak azt kell megmutatni, hogy a \(\displaystyle KFL\) szög is derékszög.
Az \(\displaystyle AB\), illetve \(\displaystyle AC\) oldal felezőpontját jelölje rendre \(\displaystyle D\) és \(\displaystyle E\). Az \(\displaystyle EF\) szakasz az \(\displaystyle ABC\) háromszög \(\displaystyle AB\)-vel párhuzamos középvonala, hossza megegyezik a \(\displaystyle DK\) szakaszéval, amely viszont \(\displaystyle AB\)-re merőleges. Hasonlóképpen \(\displaystyle DF\) és \(\displaystyle EL\) is egymásra merőleges egyenlő hosszúságú szakaszok. Ezenfelül
\(\displaystyle KDF\angle=KDB\angle+BDF\angle=90^\circ+BAC\angle=CEL\angle+FEC\angle=FEL\angle.\)
Ez azt jelenti, hogy \(\displaystyle KDF\) és \(\displaystyle FEL\) olyan egybevágó háromszögek, melyekben az egymásnak megfelelő oldalak egymásra merőlegesek. Következésképpen az \(\displaystyle FL\) szakasz is merőleges a \(\displaystyle KF\) szakaszra.
Statistics:
70 students sent a solution. 4 points: 62 students. 3 points: 4 students. 1 point: 3 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, March 2012
