 Problem B. 4444. (April 2012)
Problem B. 4444. (April 2012)
B. 4444. The points E and G, respectively, are obtained by rotating vertex D of a square ABCD about A and vertex B (lying opposite D) about C outwards, through the same acute angle  . The intersection of lines AE and BG is F. Line GD intersects the circles GCB and BDE again at points L and M, respectively. Prove that the points A, B, F, L, M are cyclic.
. The intersection of lines AE and BG is F. Line GD intersects the circles GCB and BDE again at points L and M, respectively. Prove that the points A, B, F, L, M are cyclic.
Suggested by J. Bodnár
(3 pont)
Deadline expired on May 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel a DC=CB=CG és , a DCG egyenlőszárú háromszögben
, ahonnan
következik. Mivel AE=AD=AB, a BDE kör középpontja A és így AM=AD is teljesül. Az ADM egyenlőszárú háromszögben tehát
, vagyis az ABM egyenlőszárú háromszögben
és
. Ugyanakkor az ezzel egybevágó CBG háromszögben
, ezért az ABF háromszögben
, míg
, tehát
, ami az AMB szöget 180o-ra egészíti ki. Ez azt jelenti, hogy az AFBM négyszög húrnégyszög.
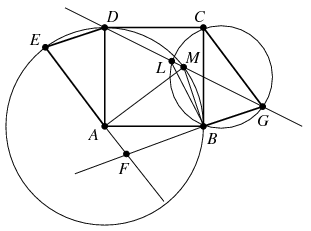
Már csak azt kell belátni, hogy az L pont is az ABM körre esik. Ez nyilvánvaló, ha L=M. Mivel a BGCL négyszög húrnégyszög, . Ha az L pont az MG szakasz belsejébe esik, akkor
, vagyis az ABLM négyszög húrnégyszög. Ha pedig L a DG egyenesen az M pont másik oldalára esik, akkor
, így most az ABML négyszög lesz húrnégyszög.
Statistics:
48 students sent a solution. 3 points: Balogh Tamás, Baumgartner Róbert, Bingler Arnold, Bősze Zsuzsanna, Czipó Bence, Emri Tamás, Énekes Tamás, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Janzer Barnabás, Janzer Olivér, Kaprinai Balázs, Khayounti Sára, Leitereg András, Maga Balázs, Nagy-György Pál, Petrényi Márk, Schultz Vera Magdolna, Schwarcz Tamás, Szabó 928 Attila, Szőke Tamás, Weimann Richárd, Weisz Ambrus, Zilahi Tamás, Zsiros Ádám. 2 points: Di Giovanni Márk, Dinev Georgi, Jávorszky Natasa, Kiss 902 Melinda Flóra, Leitereg Miklós, Makk László, Mihálykó András, Mogyorósi Ferenc, Nagy Anna Noémi, Nguyen Anh Tuan, Onódi Péter, Sagmeister Ádám, Somogyvári Kristóf, Szabó 157 Dániel, Wiandt Péter. 1 point: 3 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, April 2012
