 Problem B. 4445. (April 2012)
Problem B. 4445. (April 2012)
B. 4445. A convex solid has six square faces and eight regular hexagonal faces. Given that no two square faces have a vertex in common, and the solid has an edge of unit length, determine the volume of the solid.
(4 pont)
Deadline expired on May 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ha egy konvex poliéder valamely csúcsánál összeadjuk a csúcsban összefutó lapokra az egyes lapoknak az adott csúcsnál mért szögét, az eredmény kisebb, mint 360o. Ezért a hatszöglapok közül semelyik háromnak nem lehet közös csúcsa, tehát a poliéder minden csúcsában pontosan egy négyzetlap és két hatszöglap találkozik. Konvex poliéderről lévén szó, ez a feltétel a testet, ha ilyen létezik, egybevágóság erejéig egyérteműen meghatározza.
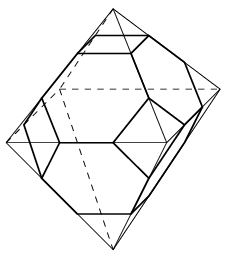
Egy ilyen testet kapunk akkor, ha egy 3 egység élű szabályos oktaéder élharmadoló pontjainak konvex burkát vesszük. Ezt megkaphatjuk oly módon is, hogy az oktaéder minden csúcsánál lemetszünk abból egy olyan négyzet alapú gúlát, melynek minden éle egységnyi hosszú. Két ilyen kis gúla egy egységnyi élű szabályos oktaéderré illeszthető össze, melynek testátlói hosszúak, és mindegyik merőleges a fennmaradó négy csúcs által meghatározott négyzet síkjára. Egy ilyen kis oktaéder térfogata tehát
. Az eredeti oktaéder térfogata ennek 27-szerese, vagyis a konvex test térfogata
Statistics:
49 students sent a solution. 4 points: Ágoston Péter, Árkos Gergely, Baumgartner Róbert, Bingler Arnold, Böszörményi Borbála, Brányi Balázs, Czipó Bence, Demeter Dániel, Di Giovanni Márk, Emri Tamás, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Gyarmati Máté, Havasi 0 Márton, Herczeg József, Homonnay Bálint, Kaprinai Balázs, Katona Dániel, Kecskés Boglárka, Kiss Botond József, Leitereg András, Leitereg Miklós, Lucskai Gábor, Maga Balázs, Makk László, Mihálykó András, Nagy Róbert, Németh 722 Noémi, Onódi Péter, Schultz Vera Magdolna, Schwarcz Tamás, Solti Bálint, Somogyvári Kristóf, Strenner Péter, Szabó 789 Barnabás, Tossenberger Tamás, Weimann Richárd, Zahemszky Péter. 3 points: Jávorszky Natasa, Kúsz Ágnes, Lelkes János, Mócsy Miklós, Stein Ármin, Thamó Emese. 2 points: 3 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, April 2012
