 |
A B. 4454. feladat (2012. május) |
B. 4454. Az ABCD paralelogrammában AB>BC. Szerkesszük meg a paralelogramma belsejében azt a P pontot, amelyre
és
(4 pont)
A beküldési határidő 2012. június 11-én LEJÁRT.
Megoldás. Tekintsük a feladatot megoldottnak. Toljuk el a P pontot a vektorral a Q pontba. Mivel P a paralelogramma belsejében van, az AD és PQ szakaszok metszik egymást. Lévén
, az első feltétel szerint
, ami azt jelenti, hogy az APDQ négyszög húrnégyszög. Ennélfogva
, vagyis a második feltétel szerint
. Az AB-vel megegyező hosszúságú PQ szakasz tehát a Thalesz-tétel megfordítása szerint az APDQ négyszög köré írható kör egyik átmérője.
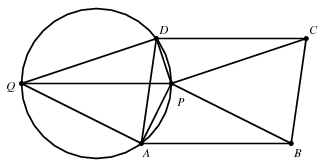
Ennek alapján a szerkesztést a következőképpen hajthatjuk végre. Először megszerkesztünk egy olyan kört, amely áthalad az A,D pontokon, sugara pedig fele az AB szakasz hosszának. Az AB>BC feltétel miatt ilyen kör létezik, mégpedig kettő is, és azok az AD szakasz felezőpontjára szimmetrikusan helyezkednek el. Ezután megszerkesztjük a körnek AB-vel párhuzamos átmérőjét; ennek a paralelogramma belsejébe eső végpontja lehet csak a keresett P pont. A fentiekből világos, hogy az így nyert pont valóban megoldása a feladatnak.
A feladatnak tehát pontosan akkor van, mégpedig két megoldása, ha a szóban forgó átmérő az AB és CD egyenesek közé esik, ami ekvivalens azzal, hogy .
Statisztika:
36 dolgozat érkezett. 4 pontot kapott: Antal Dóra, Balogh Artúr György, Bősze Zsuzsanna, Dinev Georgi, Fehér Zsombor, Fonyó Viktória, Havasi 0 Márton, Herczeg József, Janzer Barnabás, Janzer Olivér, Kiss 902 Melinda Flóra, Maga Balázs, Medek Ákos, Mester Márton, Mogyorósi Ferenc, Nagy Róbert, Nemes György, Sagmeister Ádám, Schwarcz Tamás, Szabó 789 Barnabás, Zilahi Tamás. 3 pontot kapott: Balogh Tamás, Bingler Arnold, Bősze Zsófia, Englert Franciska, Forrás Bence, Gyarmati Máté, Nguyen Anh Tuan, Trócsányi Péter, Weimann Richárd. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2012. májusi matematika feladatai

