 |
A B. 4456. feladat (2012. május) |
B. 4456. Legyen f a pozitív valós számok halmazán értelmezett olyan valós értékű függvény, amelyre
teljesül minden x,y>0 értékre. Bizonyítsuk be, hogy f konstans.
Javasolta: Daróczy Zoltán (Debrecen)
(3 pont)
A beküldési határidő 2012. június 11-én LEJÁRT.
Megoldás. Tetszőleges 0<v<1 esetén legyen x=1-u és y=1+u, ahol . Ekkor
vagyis f konstans a (0,1] intervallumon. Ahhoz, hogy belássuk, hogy f az [1,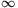 ] intervallumon, következésképpen a teljes értelmezési tartományon konstans, elegendő minden 1<a számhoz találni olyan x pozitív számot melyre x+1/x=2a, ekkor ugyanis az y=1/x választással
] intervallumon, következésképpen a teljes értelmezési tartományon konstans, elegendő minden 1<a számhoz találni olyan x pozitív számot melyre x+1/x=2a, ekkor ugyanis az y=1/x választással
fog teljesülni. Ehhez az x2-2ax+1=0 másodfokú egyenletet kell megoldanunk. Az egyenlet gyökei . Mivel ezek pozitív számok, bármelyikük választható x-nek (a másik pedig y=1/x-nek).
Statisztika:
76 dolgozat érkezett. 3 pontot kapott: Ágoston Péter, Ágoston Tamás, Almási Péter, Árkos Gergely, Babik Bálint, Badacsonyi István András, Balogh Tamás, Bingler Arnold, Csernák Tamás, Czipó Bence, Di Giovanni Márk, Énekes Tamás, Fehér Zsombor, Fonyó Viktória, Győrfi 946 Mónika, Havasi 0 Márton, Homonnay Bálint, Janzer Barnabás, Jávorszky Natasa, Kaprinai Balázs, Katona Dániel, Kiss 902 Melinda Flóra, Leitereg András, Leitereg Miklós, Maga Balázs, Makk László, Medek Ákos, Mester Márton, Mihálykó András, Mócsy Miklós, Nagy-György Pál, Papp Roland, Sagmeister Ádám, Schultz Vera Magdolna, Schwarcz Tamás, Solti Bálint, Somogyvári Kristóf, Strenner Péter, Szabó 789 Barnabás, Szabó 928 Attila, Thamó Emese, Tossenberger Tamás, Varga 911 Szabolcs, Viharos Andor, Weisz Ambrus, Zilahi Tamás. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 13 versenyző.
A KöMaL 2012. májusi matematika feladatai

