 Problem B. 4458. (May 2012)
Problem B. 4458. (May 2012)
B. 4458. Lines a and b are given lines in the plane, A is a given point not lying on a, and B is a given point not lying on b. If point O does not coincide with A or B, then there exists a transformation composed of a rotation about O and a central enlargement from O, such that A is mapped to B. What is the locus of those points in the plane for which this transformation maps the intersection of lines OA and a to the intersection of lines OB and b?
Suggested by A. Hraskó, Budapest
(4 pont)
Deadline expired on June 11, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ha az O pont ráesik valamelyik egyenesre, akkor a másik egyenesre is rá kell essen, és fordítva, ha O mindkét egyenesnek pontja, akkor a mértani helyhez tartozik. Ha O nem esik rá egyik egyenesre sem és az a egyenesnek ugyanazon az oldalán van, mint A, akkor a b egyenesnek is ugyanazon az oldalán kell legyen, mint B és fordítva, ha az a-nak a másik oldalán van, mint A, akkor a b-nek is másik oldalán kell legyen, mint B. A továbbiakban feltesszük, hogy ez teljesül.
Az A, illetve O pont távolságát az a egyenestől jelölje rendre dA és da, a B, illetve O pont távolságát a b egyenestől pedig rendre dB és db, az OA egyenesnek a-val alkotott metszéspontját A', az OB egyenesnek b-vel alkotott metszéspontját pedig B'. értelmezési problémák elkerülése végett csak olyan O pontok mértani helyét keressük, melyekre az A',B' metszéspontok léteznek. Az O pont pontosan akkor tartozik a mértani helyhez, ha OA':OA=OB':OB, vagyis ha
Ha az a és b egyenesek egybeesnek, akkor da=db, tehát szükséges, hogy dA=dB legyen. Ha A és B az a=b egyenesnek különböző oldalára esnek, akkor O nem eshet az egyenesnek egyik oldalára sem. Ekkor tehát a mértani hely az a=b egyenes. Ha pedig ugyanarra az oldalra esnek, akkor O bármelyik oldalra is essen, a fenti feltétel teljesül, viszont ha O az AB egyenesre esik, akkor az A',B' metszéspontok nem léteznek. Ekkor tehát a mértani hely az AB egyenes kivételével a teljes sík lesz.
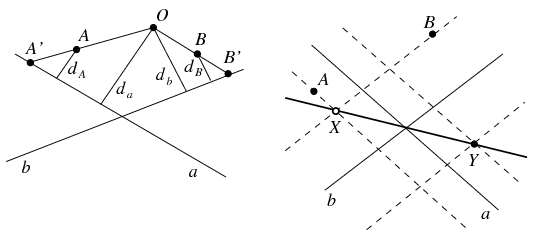
Legyen tehát a b. Húzzuk meg az a és b egyenesekkel párhuzamos, azoktól rendre dA, illetve dB távolságban haladó egyeneseket. Ez a négy egyenes négy metszéspontot határoz meg, ezek közül kettő, X és Y esik megfelelő síknegyedbe. Jelölje X azt, amelyik a-nak ugyanarra az oldalára esik, mint A és B-nek is ugyanarra az oldalára esik, mint B; az Y pont ennek az a és b egyenesek metszéspontjára vett tükörképe. Azok a pontok, melyekre az arányossági feltétel teljesül (és a megfelelő síknegyedben, vagy az a és b egyenesek metszéspontjában vannak), éppen az XY egyenes pontjai. X nem tartozik a mértani helyhez, mert az XA egyenes nem metszi a-t. Az XY egyenes csak akkor halad át az A vagy B ponton, ha az a pont egybeesik X-szel. Ekkor tehát a mértani hely az X pont kivételével a teljes XY egyenes lesz.
b. Húzzuk meg az a és b egyenesekkel párhuzamos, azoktól rendre dA, illetve dB távolságban haladó egyeneseket. Ez a négy egyenes négy metszéspontot határoz meg, ezek közül kettő, X és Y esik megfelelő síknegyedbe. Jelölje X azt, amelyik a-nak ugyanarra az oldalára esik, mint A és B-nek is ugyanarra az oldalára esik, mint B; az Y pont ennek az a és b egyenesek metszéspontjára vett tükörképe. Azok a pontok, melyekre az arányossági feltétel teljesül (és a megfelelő síknegyedben, vagy az a és b egyenesek metszéspontjában vannak), éppen az XY egyenes pontjai. X nem tartozik a mértani helyhez, mert az XA egyenes nem metszi a-t. Az XY egyenes csak akkor halad át az A vagy B ponton, ha az a pont egybeesik X-szel. Ekkor tehát a mértani hely az X pont kivételével a teljes XY egyenes lesz.
Statistics:
23 students sent a solution. 4 points: Di Giovanni Márk, Forrás Bence, Kabos Eszter, Maga Balázs, Ódor Gergely, Tossenberger Tamás. 3 points: Bingler Arnold, Janzer Barnabás, Janzer Olivér, Jávorszky Natasa, Medek Ákos, Zilahi Tamás. 2 points: 10 students. 1 point: 1 student.
Problems in Mathematics of KöMaL, May 2012
