 |
A B. 4458. feladat (2012. május) |
B. 4458. Adottak az a és b egyenesek, valamint az a-ra nem illeszkedő A és a b-re nem illeszkedő B pont. Ha O nem esik egybe az A, B pontok egyikével sem, akkor van egy olyan O centrumú forgatva nyújtás, ami A-t B-be viszi. Mi azon O pontok mértani helye a síkban, amelyekre ennél a transzformációnál az OA és az a egyenes metszéspontjának képe az OB és a b metszéspontja?
Javasolta: Hraskó András (Budapest)
(4 pont)
A beküldési határidő 2012. június 11-én LEJÁRT.
Megoldás. Ha az O pont ráesik valamelyik egyenesre, akkor a másik egyenesre is rá kell essen, és fordítva, ha O mindkét egyenesnek pontja, akkor a mértani helyhez tartozik. Ha O nem esik rá egyik egyenesre sem és az a egyenesnek ugyanazon az oldalán van, mint A, akkor a b egyenesnek is ugyanazon az oldalán kell legyen, mint B és fordítva, ha az a-nak a másik oldalán van, mint A, akkor a b-nek is másik oldalán kell legyen, mint B. A továbbiakban feltesszük, hogy ez teljesül.
Az A, illetve O pont távolságát az a egyenestől jelölje rendre dA és da, a B, illetve O pont távolságát a b egyenestől pedig rendre dB és db, az OA egyenesnek a-val alkotott metszéspontját A', az OB egyenesnek b-vel alkotott metszéspontját pedig B'. értelmezési problémák elkerülése végett csak olyan O pontok mértani helyét keressük, melyekre az A',B' metszéspontok léteznek. Az O pont pontosan akkor tartozik a mértani helyhez, ha OA':OA=OB':OB, vagyis ha
Ha az a és b egyenesek egybeesnek, akkor da=db, tehát szükséges, hogy dA=dB legyen. Ha A és B az a=b egyenesnek különböző oldalára esnek, akkor O nem eshet az egyenesnek egyik oldalára sem. Ekkor tehát a mértani hely az a=b egyenes. Ha pedig ugyanarra az oldalra esnek, akkor O bármelyik oldalra is essen, a fenti feltétel teljesül, viszont ha O az AB egyenesre esik, akkor az A',B' metszéspontok nem léteznek. Ekkor tehát a mértani hely az AB egyenes kivételével a teljes sík lesz.
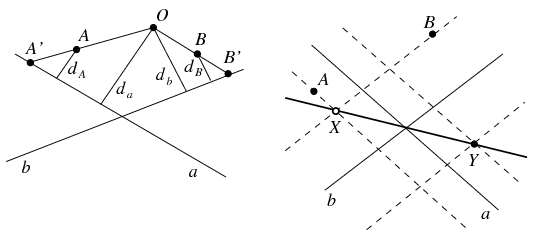
Legyen tehát a
b. Húzzuk meg az a és b egyenesekkel párhuzamos, azoktól rendre dA, illetve dB távolságban haladó egyeneseket. Ez a négy egyenes négy metszéspontot határoz meg, ezek közül kettő, X és Y esik megfelelő síknegyedbe. Jelölje X azt, amelyik a-nak ugyanarra az oldalára esik, mint A és B-nek is ugyanarra az oldalára esik, mint B; az Y pont ennek az a és b egyenesek metszéspontjára vett tükörképe. Azok a pontok, melyekre az arányossági feltétel teljesül (és a megfelelő síknegyedben, vagy az a és b egyenesek metszéspontjában vannak), éppen az XY egyenes pontjai. X nem tartozik a mértani helyhez, mert az XA egyenes nem metszi a-t. Az XY egyenes csak akkor halad át az A vagy B ponton, ha az a pont egybeesik X-szel. Ekkor tehát a mértani hely az X pont kivételével a teljes XY egyenes lesz.
Statisztika:
23 dolgozat érkezett. 4 pontot kapott: Di Giovanni Márk, Forrás Bence, Kabos Eszter, Maga Balázs, Ódor Gergely, Tossenberger Tamás. 3 pontot kapott: Bingler Arnold, Janzer Barnabás, Janzer Olivér, Jávorszky Natasa, Medek Ákos, Zilahi Tamás. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2012. májusi matematika feladatai