 Problem B. 4462. (September 2012)
Problem B. 4462. (September 2012)
B. 4462. Processed cheese is often sold in small blocks of eight identical cylindrical sectors packed together in a cylindrical box (see the figure). Each small block is individually wrapped and has a label on top. We have two boxes of such cheese: one box with peperoni flavour and another with bear's leek flavour. The boxes are turned over so that the contents are mixed on the table. Then the 16 blocks are returned to the boxes in a random arrangement (with labels all facing upwards). In how many different ways is that possible if arrangements obtained from each other by rotation are not considered different but the two boxes are distinguished?
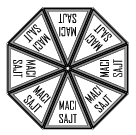
Suggested by L. Koncz, Budapest
(4 pont)
Deadline expired on October 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelölje fn azon lehetőségek számát ahányféleképpen n darab paprikásszalámis és 8-n darab medvehagymás cikkelyt el tudunk rendezni egy dobozba úgy, hogy a forgatással egymásba vihető elrendezéseket nem tekintjük különbözőnek. Nyilván fn=f8-n és ha az első dobozba n darab paprikásszalámis sajt kerül, akkor a másodikba 8-n. Ezért a különböző lehetőségek száma
Nyilván f0=f1=1, továbbá f2=4, hiszen a két darab paprikásszalámis sajt között 0,1,2, vagy 3 hely maradhat ki. Azt sem nehéz megállapítani, hogy f3=7 és f4=10. Ha 3 darab paprikásszalámis sajt kerül a dobozba, akkor egy lehetőség az, hogy közvetlenül egymás mellett vannak, 4 olyan elrendezés van melyben kettő szomszédos, de a harmadik nem szomszédos egyikkel sem, és két olyan elrendezés van, amelyben semelyik kettő nem szomszédos. Ha pedig 4 darab paprikásszalámis sajt kerül a dobozba, akkor egy lehetőség az, hogy mind a 4 egymás mellett van, 3 olyan elrendezés van, melyben 3 egymás mellett van, de a negyedik nem, 3 olyan elrendezés van, melyben pontosan két sajt van, amelyik szomszédos, két olyan elrendezés van, melyben a sajtok két szomszédos párt alkotnak, és végül egy olyan elrendezés van, amelyben semelyik kettő nem szomszédos. Ezek szerint
L=2.(1+1+16+49)+100=234.
Statistics:
232 students sent a solution. 4 points: 116 students. 3 points: 34 students. 2 points: 35 students. 1 point: 30 students. 0 point: 17 students.
Problems in Mathematics of KöMaL, September 2012
