 Problem B. 4463. (September 2012)
Problem B. 4463. (September 2012)
B. 4463. In the Four-square Round Forest, trees form a regular triangular lattice. Is it possible to build a fence around a rectangular part of the forest such that the vertices of the rectangle are lattice points and the number of lattice points on the boundary of the rectangle is the same as in the interior?
(4 pont)
Deadline expired on October 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Igen (feltéve, hogy az erdő elég nagy). Egy ilyen elkerített rész látható az ábrán, ahol mind a téglalap határán, mind annak belsejében egyaránt 14 fa áll.
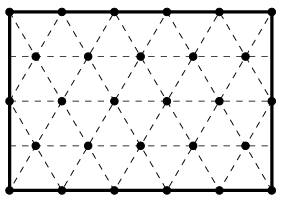
Ezt a téglalapot az alábbi gondolatmenettel találhatjuk meg. Legyen a rácspontok távolsága egységnyi és kerítsünk körbe egy -es téglalapot úgy, hogy k,n pozitív egészek és a k hosszú oldalakon, a végpontokat is beleértve, egyenként k+1 rácspont van. Ekkor az összes bekerített rácspont száma (k+1)(n+1)+kn, a határon lévők száma pedig 2(k+n), vagyis a (k+1)(n+1)+kn=4(k+n) egyenletet kell megoldanunk. Ez ekvivalens a (3k-1)(3n-1)=7kn egyenlettel, ahol 3k-1 relatív prím k-hoz, 3n-1 pedig n-hez. Tehát vagy k=3n-1 és 3k-1=7n, vagy fordítva. Az első esetben n=2 és k=5, ez látható az ábrán.
Statistics:
209 students sent a solution. 4 points: 65 students. 3 points: 27 students. 2 points: 78 students. 1 point: 20 students. 0 point: 19 students.
Problems in Mathematics of KöMaL, September 2012
