 Problem B. 4470. (September 2012)
Problem B. 4470. (September 2012)
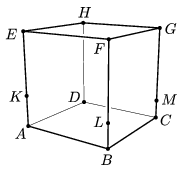
B. 4470. The cube ABCDEFGH is standing on the table. Three vertical edges are divided by the points K, L and M in ratios of 1:2, 1:3 and 1:4, respectively, as shown in the figure. The plane KLM divides the cube into two parts. What is the ratio of the volumes of the two parts?
(5 pont)
Deadline expired on October 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Feltehető, hogy a kocka élei egységnyi hosszúak; ekkor AK=1/3, BL=1/4, CM=1/5. Legyen N a DH él azon pontja, amelyre DN=1/3-1/4+1/5. Ekkor , vagyis a K,L,M,N pontok egysíkúak, ami azt jelenti, hogy a KLM sík a DH élet N-ben metszi. Toljuk el a K és N pontokat lefelé 1/3-1/4=1/12 távolsággal. Ekkor az AK, illetve DN szakasz azon K',N' pontjaihoz jutunk, melyekre AK'=BL=1/4, DN'=CM=1/5. Mivel
, a K,K',L,N,N',M pontok egy olyan háromszög alapú ferde hasáb csúcsai, melynek magassága 1, alapja pedig a KK'L háromszög, melynek területe KK'/2=1/24. Így a hasáb térfogata is 1/24.
A kocka KLMN sík alatti részéből ezt a hasábot eltávolítva a BCMLADN'K' egyenes hasábot kapjuk, melynek magassága 1, alapja pedig a BCML trapéz, melynek területe (LB+CM)/2=9/40. Így ennek a hasábnak a térfogata 9/40.
A kocka KLMN sík alatti részének térfogata tehát 1/24+9/40=32/120=4/15. A KLMN sík fölötti rész térfogata ennek megfelelően 11/15, a két rész térfogatának aránya pedig 4:11.
Statistics:
145 students sent a solution. 5 points: 56 students. 4 points: 44 students. 3 points: 24 students. 2 points: 13 students. 1 point: 8 students.
Problems in Mathematics of KöMaL, September 2012
