Problem B. 4474. (October 2012)

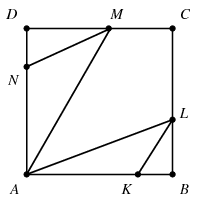
B. 4474. The points K, L, M and N, respectively, lie on sides AB, BC, CD and DA of a square ABCD. Given that $\angle$ KLA= $\angle$ LAM= $\angle$ AMN=45^o, prove that KL²+AM²=LA²+MN².

(4 pont)

Deadline expired on November 12, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Útmutatás: Lássuk be, hogy KB=DN.

Megoldás: Mivel az MAL és az AMN szögek váltószögek, az NM és AL egyenesek párhuzamosak. Ebből következik, hogy az MDN háromszög hasonló az ABL háromszöghöz. Ugyanígy az LBK háromszög hasonló az ADM háromszöghöz.

E két hasonlóság, valamint AB=AD alapján

$ND=\frac{MD}{AB}\cdot LB=\frac{LB}{AD}\cdot MD=KB.$

Ennélfogva

KL²+AM²=(KB²+LB²)+(AD²+MD²)=

=(AB²+LB²)+(ND²+MD²)=LA²+MN².

Statistics:

195 students sent a solution.

4 points: 127 students.

3 points: 27 students.

2 points: 20 students.

1 point: 14 students.

0 point: 5 students.

Unfair, not evaluated: 2 solutionss.

Problems in Mathematics of KöMaL, October 2012

195 students sent a solution.
4 points:	127 students.
3 points:	27 students.
2 points:	20 students.
1 point:	14 students.
0 point:	5 students.
Unfair, not evaluated:	2 solutionss.

Already signed up?
New to KöMaL?