 Problem B. 4475. (October 2012)
Problem B. 4475. (October 2012)
B. 4475. Prove that for every convex polyhedron with five faces there exists a plane that does not pass through any vertex but intersects each face.
Suggested by V. Vígh, Szeged
(5 pont)
Deadline expired on November 12, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Útmutatás: Lássuk be, hogy kombinatorikusan pontosan kétféle ötlapú konvex poliéder van.
Megoldás: Legyen K egy ötlapú konvex poliéder, ekkor K minden lapjának legfeljebb 4 éle van. K-nak biztosan van legalább egy négyszöglapja. Ha ugyanis K-nak minden lapja háromszög lenne, akkor éleinek száma (5.3)/2=7,5 lenne, ami lehetetlen. Legyen K-nak egy négyszöglapja ABCD. Ha ennek valamennyi élére háromszöglap illeszkedik, akkor azoknak egy közös E csúcsban kell összefutni, vagyis egy négyszög alapú gúláról van szó. Ha pedig az AB élre egy ABEF négyszöglap illeszkedik, akkor az EF élet nem tartalmazhatja sem a BC-re sem az AD-re illeszkedő lap, tehát csak a CD élre illeszkedő lap tartalmazhatja, vagyis egy háztető-szerű testről van szó.
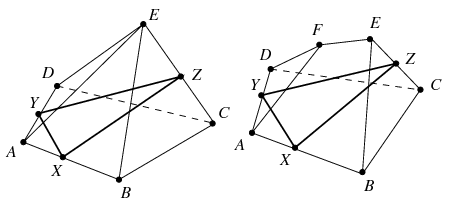
Bármelyik esetről legyen is szó, vegyünk fel az AB, AD, CE élek belsejében egy-egy X, Y, Z pontot az ábra szerint. Ezek nem esnek egy egyenesre, és az általuk meghatározott sík nem tartalmazza K-nak egyetlen élét sem. Mivel az XYZ síknak a K poliéder minden lapjával van csúcstól különböző közös pontja, annak mind az 5 lapját metszi.
Statistics:
67 students sent a solution. 5 points: Ágoston Péter, Árkos Gergely, Badacsonyi István András, Baran Zsuzsanna, Barna István, Baumgartner Róbert, Bingler Arnold, Énekes Tamás, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Forrás Bence, Havasi 0 Márton, Herczeg József, Homonnay Bálint, Janzer Barnabás, Janzer Olivér, Jávorszky Natasa, Kabos Eszter, Kúsz Ágnes, Leitereg András, Leitereg Miklós, Maga Balázs, Medek Ákos, Mócsy Miklós, Schultz Vera Magdolna, Szabó 262 Lóránt, Szabó 789 Barnabás, Szász Dániel Soma, Tossenberger Tamás, Venczel Tünde, Williams Kada, Zilahi Tamás. 4 points: Balogh Tamás, Bognár Máté, Csibi Levente, Gergely Anita, Németh Gergely, Petrényi Márk, Sagmeister Ádám, Sal Kristóf, Schwarcz Tamás, Tardos Jakab, Tóth László Gábor. 3 points: 6 students. 2 points: 10 students. 1 point: 4 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, October 2012
