 Problem B. 4480. (October 2012)
Problem B. 4480. (October 2012)
B. 4480. The escribed circle drawn to side AB of a triangle ABC touches the lines of sides AB, BC and CA at the points E, F, G, respectively. The intersection of lines AF and BG is H. The inscribed circle of the triangle formed by the midlines of triangle ABC touches the side parallel to AB at point N. Prove that the points E, H and N are collinear.
Suggested by Sz. Miklós, Herceghalom
(5 pont)
Deadline expired on November 12, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Útmutatás: C pont is illeszkedik az egyenesre.
Megoldás: A háromszög oldalait és kerületének felét a szokásos módon jelölje a,b,c,s. Mivel AE=AG és BE=BF, CF+CG=a+b+c, ahonnan CF=CG=s, AE=AG=s-b és BE=BF=s-a. Ennek következtében
Ez akkor is fennáll, ha előjeles szakaszokkal számolunk, hiszen pontosan két szakasz (BF és GA) előjele lesz negatív. Ceva tételének megfordítása szerint az AF, BG és CE egyenesek egy pontban metszik egymást, ami éppen a H pont. Eszerint tehát az egymástól különböző C,E és H pontok egy egyenesre illeszkednek. Már csak annyit kell belátni, hogy az egymástól különböző C,E és N pontok is egy egyenesre illeszkednek.
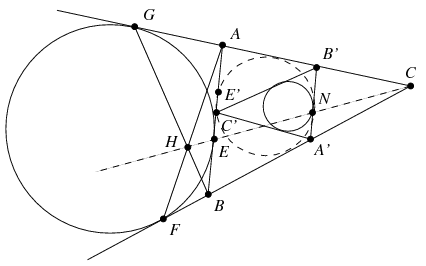
Az ABC háromszögbe írható kör érintse az AB oldalt az E' pontban. Közismert (és a fenti módszerrel könnyen igazolható), hogy AE'=s-a és BE'=s-b. Az ABC háromszög és a középvonalai által meghatározott A'B'C' háromszög hasonlóságából A'N:B'N=AE':BE'=BE:AE. A B'A'C háromszöget megkaphatjuk az ABC háromszögből ha azt a C pontból felére kicsinyítjük. A fenti arányosság miatt ez a transzformáció az E pontot az N-be viszi, vagyis N éppen a CE szakasz felezőpontja. Ezzel az állítást igazoltuk.
Statistics:
36 students sent a solution. 5 points: Ágoston Péter, Balogh Tamás, Bingler Arnold, Bogár Blanka, Bősze Zsuzsanna, Demeter Dániel, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Havasi 0 Márton, Homonnay Bálint, Janzer Barnabás, Janzer Olivér, Kúsz Ágnes, Maga Balázs, Medek Ákos, Nagy Róbert, Nagy-György Pál, Petrényi Márk, Sagmeister Ádám, Sárosdi Zsombor, Schwarcz Tamás, Szabó 262 Lóránt, Szabó 789 Barnabás, Szabó 928 Attila, Tardos Jakab, Tossenberger Tamás, Tulassay Zsolt. 4 points: Herczeg József, Nagy Bence Kristóf. 3 points: 1 student. 2 points: 3 students. 0 point: 2 students.
Problems in Mathematics of KöMaL, October 2012
