 Problem B. 4481. (October 2012)
Problem B. 4481. (October 2012)
B. 4481. Find all polynomials f of integer coefficients such that for every positive integer n the prime factors of the numbers n and f(n) coincide.
(5 pont)
Deadline expired on November 12, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Útmutatás: A konstans tag 0. Emeljük ki x-et.
Megoldás: Tetszőleges k pozitív egészre az f(x)=xk és az f(x)=-xk polinomok megfelelőek. Tegyük fel, hogy az polinom megfelelő, ahol ak
 0. Megmutatjuk, hogy ekkor k>0,
0. Megmutatjuk, hogy ekkor k>0, és ak=
 1, ami azt jelenti, hogy ezzel a feladat összes megoldását megkaptuk.
1, ami azt jelenti, hogy ezzel a feladat összes megoldását megkaptuk.
Legyen p tetszőleges (pozitív) prímszám; ilyenből végtelen sok van. A feltétel szerint létezik olyan 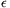 (p)=
(p)= 1 és
1 és  (p) pozitív egész, hogy
(p) pozitív egész, hogy . Mivel f(p)-a0 osztható p-vel, a0 is osztható kell legyen p-vel. Ebből következik, hogy a0 végtelen sok különböző prímszámmal osztható, vagyis a0=0, amiért is k
 0.
0.
Tegyük fel, hogy valamely 0 i<k-1 esetén már beláttuk, hogy
i<k-1 esetén már beláttuk, hogy . Ekkor
, vagyis
Mivel egy m-edfokú nemkonstans polinom legfeljebb m különböző helyen veheti fel ugyanazt az értéket, van végtelen sok olyan p prímszám, melyre az
kifejezés értéke nem  1, vagyis osztható p-vel. Ezekre a p számokra tehát ai+1 is osztható p-vel, vagyis ai+1=0.
1, vagyis osztható p-vel. Ezekre a p számokra tehát ai+1 is osztható p-vel, vagyis ai+1=0.
Így i szerinti indukcióval kapjuk, hogy , tehát f(x)=akxk. Ezért minden p-re
. Mivel ak csak véges sok különböző prímszámmal lehet osztható, végtelen sok p-re teljesül
 (p)=k, ak=
(p)=k, ak=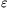 (p). Emiatt valóban ak=
(p). Emiatt valóban ak= 1, ahogyan azt állítottuk.
1, ahogyan azt állítottuk.
Statistics:
73 students sent a solution. 5 points: Barna István, Bogáromi Dávid, Di Giovanni Márk, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Janzer Barnabás, Janzer Olivér, Maga Balázs, Somogyvári Kristóf, Szabó 789 Barnabás, Tardos Jakab, Tossenberger Tamás, Vályi András, Williams Kada. 4 points: Balogh Tamás, Bereczki Zoltán, Csernák Tamás, Czipó Bence, Havasi 0 Márton, Homonnay Bálint, Kátay Tamás, Katona Dániel, Lőrinczy Zsófia Noémi, Makk László, Medek Ákos, Nagy Róbert, Nagy-György Pál, Papp Roland, Seress Dániel, Simon 047 Péter, Zarándy Álmos, Zilahi Tamás. 3 points: 6 students. 2 points: 8 students. 1 point: 16 students. 0 point: 10 students.
Problems in Mathematics of KöMaL, October 2012
