Problem B. 4494. (December 2012)

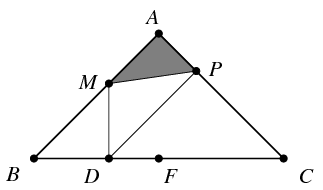
B. 4494. F is the midpoint of base BC of the isosceles triangle ABC. D is an interior point of the line segment BF. The perpendicular dropped from point D onto BC intersects side AB at M, and the line through point D, parallel to AB intersects side AC at P. Express the ratio of the areas of triangles AMP and ABC in terms of k=BD:BC.

Matlap, Cluj-Napoca - Kolozsvár, Romania

(3 pont)

Deadline expired on January 10, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Útmutatás: Fejezzük ki a területeket két oldal és a közbezárt szög segítségével.

Megoldás: A párhuzamos szelők tétele szerint AP:AC=BD:BC=k. Mivel AF párhuzamos MD-vel, $AM:AB=FD:FB=\left(\frac{1}{2}-k\right):\frac{1}{2}$ . Az AMP és ABC háromszögek A-nál lévő szöge megegyezik, ezért a két háromszög területének aránya

$\frac{AP}{AC}\cdot\frac{AM}{AB}=k(1-2k)=k-2k^2.$

Statistics:

144 students sent a solution.

3 points: 121 students.

2 points: 14 students.

1 point: 4 students.

0 point: 5 students.

Problems in Mathematics of KöMaL, December 2012

144 students sent a solution.
3 points:	121 students.
2 points:	14 students.
1 point:	4 students.
0 point:	5 students.

Already signed up?
New to KöMaL?