 Problem B. 4498. (December 2012)
Problem B. 4498. (December 2012)
B. 4498. A vertex B of a convex quadrilateral ABCD is said to be ``special'' if the reflection of line BD in the bisector of angle ABC bisects the diagonal AC. Prove that if one vertex of a cyclic quadrilateral is special then all vertices are special.
Suggested by P. Maga, Budapest
(5 pont)
Deadline expired on January 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Útmutatás: Legyen F az AC szakasz felezőpontja. Írjuk fel a szinusztételt az ABF és a BCF háromszögekre.
Megoldás: Elegendő annyit belátni, hogy ha a B csúcs különleges, akkor az A csúcs is az. Az AC, BD és AD szakaszok felezőpontját jelölje rendre F, G, illetve H. Legyen az AC szakasz felező merőlegese t. A B,D pontok t-re vett tükörképét jelölje B'',D'', továbbá legyen F' a t egyenesnek a B-t nem tartalmazó AC ívvel vett metszéspontja. Ekkor F' az AC ív felezőpontja, vagyis az a pont, amelyben a B-ből induló szögfelező az AC ívet metszi.
Az hogy a B csúcs különleges, ekvivalens tehát azzal, hogy a BD'' és B''D szakaszok áthaladnak az F ponton, vagyis hogy a CDB szög egyenlő az FDA szöggel. Az ,
,
megfeleltetés szerint pedig az A csúcs különleges volta ekvivalens azzal, hogy a DCA szög egyenlő az GCB szöggel. Annyit kell ezek szerint csak belátnunk, hogy ha CDB
 =FDA
=FDA , akkor DCA
, akkor DCA =GCB
=GCB is teljesül.
is teljesül.
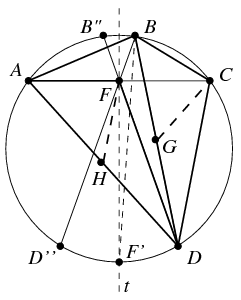
Tegyük fel tehát, hogy CDB =FDA
=FDA . Mivel a kerületi szögek tétele szerint DBC
. Mivel a kerületi szögek tétele szerint DBC =DAF
=DAF , a DBC és DAF háromszögek hasonlóak. Ezért a GBC és HAF háromszögek is hasonlóak. Mivel pedig az FH szakasz párhuzamos CD-vel, látható hogy valóban GCB
, a DBC és DAF háromszögek hasonlóak. Ezért a GBC és HAF háromszögek is hasonlóak. Mivel pedig az FH szakasz párhuzamos CD-vel, látható hogy valóban GCB =HFA
=HFA =DCA
=DCA .
.
Statistics:
30 students sent a solution. 5 points: Balogh Tamás, Bingler Arnold, Bogár Blanka, Bősze Zsuzsanna, Emri Tamás, Fehér Zsombor, Gyulai-Nagy Szuzina, Janzer Barnabás, Janzer Olivér, Kúsz Ágnes, Maga Balázs, Nagy-György Pál, Paulovics Zoltán, Petrényi Márk, Sagmeister Ádám, Simkó Irén, Simon 047 Péter, Szabó 789 Barnabás, Szabó 928 Attila, Tossenberger Tamás, Venczel Tünde. 4 points: Dinev Georgi, Herczeg József, Kabos Eszter, Medek Ákos, Nagy Róbert, Schultz Vera Magdolna. 3 points: 2 students. 2 points: 1 student.
Problems in Mathematics of KöMaL, December 2012
