Problem B. 4504. (January 2013)

B. 4504. In a right-angled triangle, the segment of the perpendicular bisector of the hypotenuse between the lines of the legs is equal in length to the hypotenuse. Determine the angles of the triangle.

(4 pont)

Deadline expired on February 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldási ötlet: Keressünk egyenlő szárú háromszögeket.

Megoldás. Legyen a háromszög átfogója AB, derékszögű csúcsa C, az átfogó felezőpontja F, a befogók egyenesei és az átfogó felező merőlegesének metszéspontja P, illetve Q, az ábra szerint. Legyen $\alpha=BAC\sphericalangle$ .

Mivel P az AB felező merőlegesén van, $PBA\sphericalangle=\alpha$ . Az ABC és a QBF derékszögű háromszögek hasonlók, mert B-nél levő szögük közös, ezért $FQB\sphericalangle=\alpha$ . Az ABC és a QPC háromszögek is hasonlók, mert két szögük megegyezik.

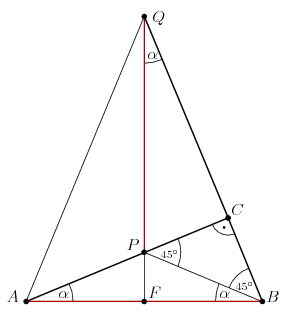
Az ABC és a QPC derékszögű háromszögek átfogója egyenlő, ezért a két háromszög egybevágó; többek közt BC=PC. A BPC háromszög tehát egyenlő szárú derékszögű háromszög, és $PBC\sphericalangle=CPB\sphericalangle=45^\circ$ . (Hasonlóan láthatjuk, hogy AC=QC, és az ACQ háromszög is egyenlő szárú derékszögű háromszög.) Ezután az ABC háromszög szögeiből leolvashatjuk, hogy $\alpha$ =22,5^o.

A lépéseink megfordíthatóak: ha $\alpha$ =22,5^o, akkor $PBC\sphericalangle=45^\circ$ , az ABC és a QPC háromszögek egybevágók, végül AB=PQ.

Az ABC háromszög szögei tehát 90^o, 22,5^o és 67,5^o.

Statistics:

205 students sent a solution.

4 points: 129 students.

3 points: 53 students.

2 points: 4 students.

1 point: 5 students.

0 point: 14 students.

Problems in Mathematics of KöMaL, January 2013

205 students sent a solution.
4 points:	129 students.
3 points:	53 students.
2 points:	4 students.
1 point:	5 students.
0 point:	14 students.

Already signed up?
New to KöMaL?