 Problem B. 4507. (January 2013)
Problem B. 4507. (January 2013)
B. 4507. The area of a regular heptagon is 4095 units. A and B are two consecutive vertices, and K is the centre of the heptagon. P is a point lying on the circumscribed circle of triangle ABK in the interior of the heptagon. Given that , what may be the area of triangle ABP?
Italian competition problem
(5 pont)
Deadline expired on February 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldási ötlet: Írjuk fel a koszinusztételt az ABK háromszögre.
1. megoldás. Legyen a hétszög köré írt kör sugara r, oldala s, PA=a, PB=b. Mivel a P pont az AKB köríven van, . Az ABP háromszög területét a
képletből fogjuk meghatározni; ehhez az ab szorzatra van szükségünk.
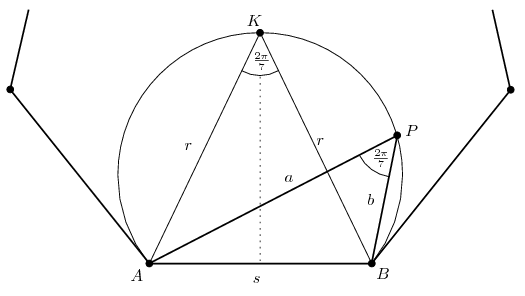
A hétszög területe , ebből kapjuk, hogy (a sin 2t=2sin tcos t azonosságot is felhasználva)
Szintén az ABK egyenlő szárú háromszögből
A feltétel szerint , ezt emeljük négyzetre:
| (1) |
Írjuk fel a koszinusztételt az ABP háromszög AB oldalára:
| (2) |
A (2) és (1) különbsége
Ezt átrendezve, behelyettesítve a korábbi eredményeket, és alkalmazva a azonosságot:
Az ABP háromszög területe tehát 325 egység.
2. megoldás. Az ABK egyenlő szárú háromszög a szabályos hétszög hetede, ezért a területe .
Legyen az AB és a KP egyenesek metszéspontja M, és legyen K, illetve P távolsága az AB egyenestől dK és dP. Mivel az ABK és az ABP háromszögek AB oldala közös, a párhuzamos szelők tételéből
A megoldáshoz a arányt fogjuk kiszámítani.
Az ABK háromszög körülírt körén legyen F az AB ív felezőpontja. Tükrözzük A-t és B-t a PF egyenesre, és jelöljük a két tükörképet A'-vel, illetve B'-vel. A kerületi szögek tétele miatt PF felezi az APB szöget, ezért A' a PB félegyenesen, B' pedig a PA félegyenesen van, és
Az AA' és BB' egyenesek a PF-re való szimmetria miatt, a KP pedig a Thalész-tétel miatt merőlegesek a PF egyenesre. Az AA', BB' és KP egyenesek tehát párhuzamosak. Ebből és az AA'P háromszög szimmetriájából láthatjuk, hogy és
, továbbá az ABPK húrnégyszögben
és
.
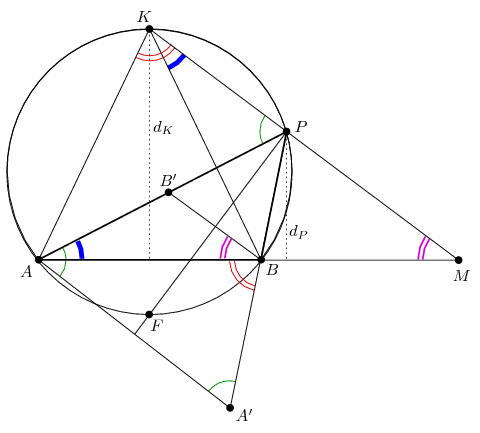
Az AKP és az ABA' háromszögek hasonlók, mert két szögük megegyezik: és
. Ezért
, így
| (3) |
A BKM és a B'AB háromszögek is hasonlók, mert és
. Ezért
, tehát
| (4) |
A (3) és (4) összevetéséből kapjuk, hogy
Tehát
Statistics:
89 students sent a solution. 5 points: Ágoston Péter, Balogh Dániel, Balogh Tamás, Baran Zsuzsanna, Bereczki Zoltán, Bingler Arnold, Bogár Blanka, Bősze Zsuzsanna, Di Giovanni Márk, Fehér Zsombor, Fekete Panna, Forrás Bence, Gyulai-Nagy Szuzina, Havasi 0 Márton, Herczeg József, Janzer Barnabás, Janzer Olivér, Kovács 148 Dávid, Kovács Balázs Marcell, Leitereg Miklós, Lelkes János, Maga Balázs, Mándoki Sára, Mócsy Miklós, Nagy Gergely, Nagy Róbert, Nagy-György Pál, Németh Gergely, Nguyen Anh Tuan, Petrényi Márk, Porupsánszki István, Sagmeister Ádám, Schultz Vera Magdolna, Schwarcz Tamás, Simkó Irén, Stein Ármin, Szabó 262 Lóránt, Szabó 789 Barnabás, Szabó 928 Attila, Szőke Tamás, Tardos Jakab, Tossenberger Tamás, Venczel Tünde, Williams Kada, Zilahi Tamás. 4 points: 18 students. 3 points: 7 students. 2 points: 2 students. 0 point: 11 students. Unfair, not evaluated: 6 solutionss.
Problems in Mathematics of KöMaL, January 2013
