 Problem B. 4513. (February 2013)
Problem B. 4513. (February 2013)
B. 4513. The radius of the circumscribed circle of an isosceles triangle of unit base is also unity. The diameter parallel to the base of the triangle cuts off a smaller triangle. Find the exact lengths of the base and legs of the smaller triangle.
Suggested by A. Balga, Budapest
(3 pont)
Deadline expired on March 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldási ötlet: Számítsuk ki a szögeket.
Megoldásvázlat. Legyen a háromszög ABC, az alapja c, a körülírt kör középontja O. Ha az AB egyenes elválasztja egymástól az O és C pontokat, akkor a körülírt kör AB-vel párhuzamos átmérője nem metszi az ABC háromszög oldalait, így ez az eset nem lehetséges (baloldali ábra). Az O és a C pontnak az AB egyenes ugyanazon az oldalán kell lennie, a jobboldali ábra szerint. Legyen a levágott háromszög DEC. Az AB oldal felezőpontját jelöljük F-fel. A szimmetria miatt az O pont felezi a DE szakaszt.
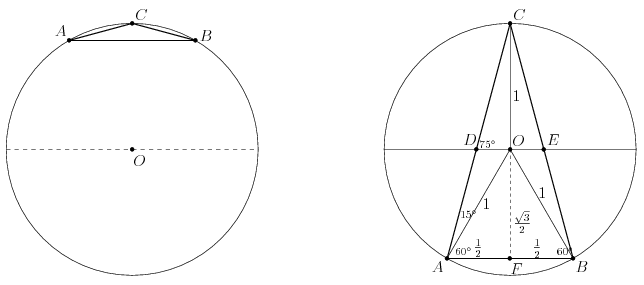
A feltétel szerint AB=OA=OB=OC=1. Az ABO háromszög szabályos, mert mindegyik oldala egységnyi; a szögei tehát 60 fokosak. Az ACO egyenlő szárú háromszögben , így
. Mivel AB||DE, azért
, és ugyanígy DEC
 =75o.
=75o.
Ismeretes, hogy a 75o szögfüggvényei a következők (ezeket például az addíciós képletekből, a 45o és 30o szögfüggvényeiből számíthatjuk ki):
A CDO és CEO derékszögű háromszögekben CO=1, ezért
és
Megjegyzés. A CD és a DE oldalak hosszát szögfüggvények nélkül is kiszámíthatjuk az AFO és AFC hároszögekre feírt a Pithagorasz-tételből, valamint az ABC és DEC háromszögek hasonlóságából.
Statistics:
189 students sent a solution. 3 points: 125 students. 2 points: 56 students. 1 point: 7 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, February 2013
