 Problem B. 4527. (March 2013)
Problem B. 4527. (March 2013)
B. 4527. In a dice game, the player rolls three dice simultaneously, and then he may roll two more times any number of his dice (0, 1, 2 or 3). The player wins the game if all three dice have the same number on top after the last roll. What is the best strategy, and with that strategy what is the probability of winning?
Suggested by E. Gáspár Merse, Budapest
(5 pont)
Deadline expired on April 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldási ötlet: A játék lehetséges állapotait rajzoljuk fel irányított gráffal.
Megoldásvázlat. Az első dobásnak három eredménye lehetséges.
I. Mindhárom egyforma. Ennek valószínűsége \(\displaystyle \frac{6}{6^3}=\frac{1}{36}\).
II. Két dobás eredménye megegyezik, a harmadik pedig ezektől különböző. Ennek valószínűsége \(\displaystyle \frac{6\cdot5\cdot3}{6^3}=\frac{5}{12}\). Ebben az esetben azzal az egy kockával dobunk újra, ami különbözik a másik kettőtől. Ekkor \(\displaystyle \frac16\) valószínűséggel nyerünk. Ha nem nyerünk, újra dobunk.
III. Mindhárom kockán különböző szám áll.
Szemléltessük a lehetőségeket irányított gráffal. "+" jel jelenti azt, hogy nyerünk, a "-", hogy nem.
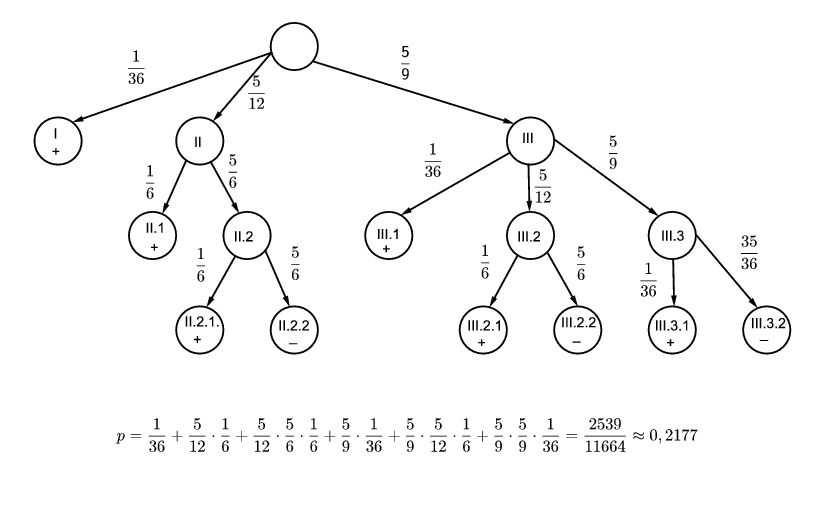
Tehát \(\displaystyle 21,77\%\) az esély arra, hogy nyerünk.
Statistics:
85 students sent a solution. 5 points: Ágoston Péter, Balogh Tamás, Baran Zsuzsanna, Bereczki Zoltán, Bingler Arnold, Csépai András, Csernák Tamás, Di Giovanni Márk, Fekete Panna, Fellner Máté, Fonyó Viktória, Forrás Bence, Havasi 0 Márton, Janzer Barnabás, Janzer Olivér, Kovács Balázs Marcell, Kúsz Ágnes, Leitereg Miklós, Maga Balázs, Mezősi Máté, Nagy Bence Kristóf, Nagy-György Pál, Németh Gergely, Osváth Tibor Attila, Paulovics Zoltán, Sagmeister Ádám, Schwarcz Tamás, Szabó 789 Barnabás, Talyigás Gergely, Tossenberger Tamás, Venczel Tünde, Weisz Ambrus, Williams Kada. 4 points: 24 students. 3 points: 15 students. 2 points: 2 students. 1 point: 3 students. 0 point: 3 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, March 2013
