Problem B. 4528. (March 2013)

B. 4528. k is the circumscribed circle of a cyclic quadrilateral ABCD. The centre of the inscribed circle of triangle ABC is P, and that of triangle ABD is Q. Let E denote the midpoint of arc BC, and let F denote the midpoint of arc DA of the circle k. Prove that PQ is parallel to EF.

(5 pont)

Deadline expired on April 10, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldási ötlet: Vegyük fel az AB ív M felezőpontját, és rajzoljuk meg az M középpontú, A-n és B-n átmenő kört.

Megoldás. Legyen M a körülírt kör C-vel szemközti AB ívének felezőpontja. Az ABC háromszögben AP és CP, az ABD háromszögben BP és CQ szögfelezők, amik átmennek a körülírt kör megfelelő ívének metszéspontján: AP átmegy E-n, az BQ egyenes F-en, a CP és DQ pedig M-en.

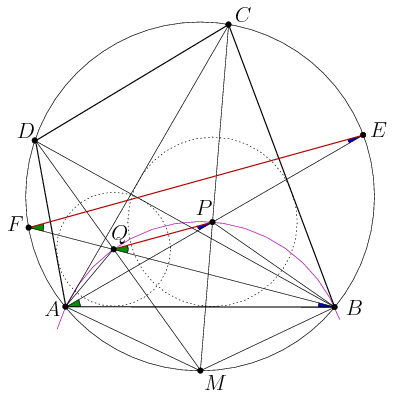
Megmutatjuk, hogy MA=MB=MP=MQ, így ABPQ húrnégyszög. Ebből MA=MB triviális, továbbá P és Q szerepe szimmetrikus, így elég például azt igazolnunk, hogy az MBP háromszög egyenlő szárú. Az ABC háromszög szögeit a szokásos módon $\alpha$ , $\beta$ , $\gamma$ -val jelölve,

$MBP\sphericalangle = MBA\sphericalangle + ABP\sphericalangle = MCA\sphericalangle + ABP\sphericalangle = \frac\gamma2 + \frac\beta2$

és

$BPM\sphericalangle = 180^\circ - CPB\sphericalangle = PBC\sphericalangle + BCP\sphericalangle = \frac\beta2 + \frac\gamma2,$

tehát valóban $MBP\sphericalangle = BPM\sphericalangle$ , és így MP=MP.

Végül a kerületi szögek tételét az ABEF és ABPQ négyszögekre alkalmazva,

$EFB\sphericalangle = EAB\sphericalangle = PAB\sphericalangle = PQA\sphericalangle.$

Ebből következik, hogy EF és PQ párhuzamos.

Statistics:

53 students sent a solution.

5 points: Ágoston Péter, Balogh Tamás, Bereczki Zoltán, Bingler Arnold, Bogár Blanka, Boguszlavszkij Gergely, Bus Tamás, Csépai András, Di Giovanni Márk, Dinev Georgi, Emri Tamás, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Győrfi 946 Mónika, Gyulai-Nagy Szuzina, Herczeg József, Hoang Ly Melinda, Janzer Barnabás, Janzer Olivér, Kúsz Ágnes, Machó Bónis, Maga Balázs, Nagy Gergely, Nagy Róbert, Nagy-György Pál, Páli Petra, Petrényi Márk, Porupsánszki István, Radó Hanna, Sagmeister Ádám, Sal Kristóf, Sárosdi Zsombor, Schultz Vera Magdolna, Schwarcz Tamás, Simkó Irén, Sütő Máté, Szabó 262 Lóránt, Szabó 789 Barnabás, Szabó 928 Attila, Szebellédi Márton, Szőke Tamás, Tardos Jakab, Tossenberger Tamás, Varga 911 Szabolcs, Venczel Tünde, Williams Kada, Zarándy Álmos, Zilahi Tamás.

2 points: 2 students.

1 point: 1 student.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, March 2013

53 students sent a solution.
5 points:	Ágoston Péter, Balogh Tamás, Bereczki Zoltán, Bingler Arnold, Bogár Blanka, Boguszlavszkij Gergely, Bus Tamás, Csépai András, Di Giovanni Márk, Dinev Georgi, Emri Tamás, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Győrfi 946 Mónika, Gyulai-Nagy Szuzina, Herczeg József, Hoang Ly Melinda, Janzer Barnabás, Janzer Olivér, Kúsz Ágnes, Machó Bónis, Maga Balázs, Nagy Gergely, Nagy Róbert, Nagy-György Pál, Páli Petra, Petrényi Márk, Porupsánszki István, Radó Hanna, Sagmeister Ádám, Sal Kristóf, Sárosdi Zsombor, Schultz Vera Magdolna, Schwarcz Tamás, Simkó Irén, Sütő Máté, Szabó 262 Lóránt, Szabó 789 Barnabás, Szabó 928 Attila, Szebellédi Márton, Szőke Tamás, Tardos Jakab, Tossenberger Tamás, Varga 911 Szabolcs, Venczel Tünde, Williams Kada, Zarándy Álmos, Zilahi Tamás.
2 points:	2 students.
1 point:	1 student.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?