 Problem B. 4530. (March 2013)
Problem B. 4530. (March 2013)
B. 4530. Prove that the midpoint of the line segment connecting the centres of two regular polygons of the same number of sides drawn on the sides AC and BC of a triangle ABC on the outside coincides with the centre of the regular polygon of the same number of sides drawn on the line segment connecting the midpoints of the sides AC and BC, on the side where the vertex C lies.
Suggested by Sz. Miklós, Herceghalom
(5 pont)
Deadline expired on April 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldási ötlet: Használjunk forgatva nyújtásokat vagy komplex számokat.
Megoldásvázlat. Helyezzük el a háromszöget a komplex számsíkon; az egyes pontokat és az őket reprezetáló komplex számokat ugyanazzal a betűvel fogjuk jelölni.
Legyen \(\displaystyle F\) a \(\displaystyle BC\) szakasz felezőpontja, azaz \(\displaystyle F=\frac{B+C}2\). Hasonlóan, legyen \(\displaystyle G=\frac{A+C}2\) az \(\displaystyle AC\) oldal felezőpontja. Legyen az \(\displaystyle AC\), \(\displaystyle BC\) és \(\displaystyle FG\) szakaszokra emelt szabályos sokszögek középpontja rendre \(\displaystyle P\), \(\displaystyle Q\), illetve \(\displaystyle R\). Azt kell igazolnunk, hogy \(\displaystyle R=\frac{P+Q}2\).
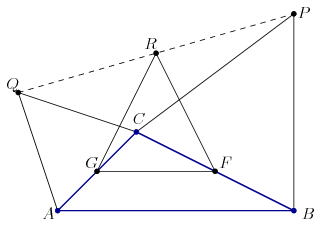
A \(\displaystyle CBP\), \(\displaystyle ACQ\) és \(\displaystyle GFR\) háromszögek hasonlók, ezért
\(\displaystyle \frac{P-C}{B-C} = \frac{Q-A}{C-A} = \frac{R-G}{F-G}; \)
jelöljük ezt a komplex számot \(\displaystyle f\)-fel. Ekkor \(\displaystyle \frac{P-C}{B-C}=f\)-ből \(\displaystyle P\)-t kifejezve:
\(\displaystyle P = f(B-C)+C = fB+(1-f)C. \)
Hasonlóan kapjuk, hogy \(\displaystyle Q=(1-f)A+fC\) és \(\displaystyle R=fF+(1-f)G\). Tehát
\(\displaystyle R = fF+(1-f)G = f\frac{B+C}2+(1-f)\frac{A+C}2 = \frac{\big(fB+(1-f)C\big) + \big((1-f)A+fC\big)}2 = \frac{P+Q}2. \)
Statistics:
51 students sent a solution. 5 points: Ágoston Péter, Balogh Tamás, Bereczki Zoltán, Bingler Arnold, Bogár Blanka, Bősze Zsuzsanna, Di Giovanni Márk, Emri Tamás, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Forrás Bence, Gyulai-Nagy Szuzina, Havasi 0 Márton, Herczeg József, Janzer Barnabás, Janzer Olivér, Kabos Eszter, Kátay Tamás, Khayouti Sára, Kovács Balázs Marcell, Kulcsár Ildikó, Kúsz Ágnes, Leipold Péter, Leitereg Miklós, Machó Bónis, Maga Balázs, Makk László, Mócsy Miklós, Nagy-György Pál, Paulovics Zoltán, Petrényi Márk, Sagmeister Ádám, Simkó Irén, Szabó 524 Tímea, Szabó 928 Attila, Szaksz Bence, Szőke Tamás, Tardos Jakab, Tossenberger Tamás, Tóth 095 Zsombor, Venczel Tünde, Williams Kada, Zahemszky Péter, Zilahi Tamás. 4 points: Győrfi 946 Mónika, Lelkes János, Porupsánszki István, Seress Dániel. 3 points: 2 students.
Problems in Mathematics of KöMaL, March 2013
