 Problem B. 4534. (April 2013)
Problem B. 4534. (April 2013)
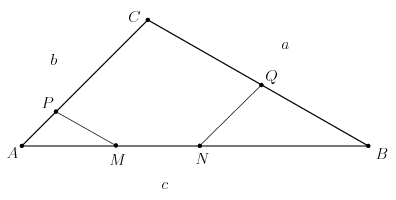
B. 4534. M and N are points on the longest side, AB of a triangle ABC, such that BM=BC and AN=AC. The parallel drawn through point M to the side BC intersects side AC at P, and the parallel drawn through point N to the side AC intersects side BC at Q. Prove that CP=CQ.
(Kvant)
(3 pont)
Deadline expired on May 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldási ötlet: Párhuzamos szelők tétele.
Megoldás. Legyenek a háromszög oldalai BC=a, CA=b és AB=c. A párhuzamos szelők tételét alkamazva, , amiből
Hasonlóan kapjuk, hogy , és
Tehát .
Statistics:
100 students sent a solution. 3 points: 94 students. 2 points: 1 student. 1 point: 2 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, April 2013
