Problem B. 4536. (April 2013)

B. 4536. Point P lies in the plane of a triangle ABC. The orthogonal projections of P onto the altitudes of the triangle are A₁, B₁ and C₁. Given that AA₁=BB₁=CC₁, determine the point P, and find the equal length of these three line segments.

(5 pont)

Deadline expired on May 10, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldási ötlet: Hol vannak azok a pontok, amikor pl. AA₁=BB₁?

Megoldásvázlat: Legyen A', B' és C' az A, B, illetve C tükörképe a szemközti oldal középpontjára. Megmutatjuk, hogy AA₁=BB₁ akkor és csak akkor teljesül, ha P az A'B'C' háromszög valamelyik C-ből induló (belső vagy külső) szögfelezőjén van.

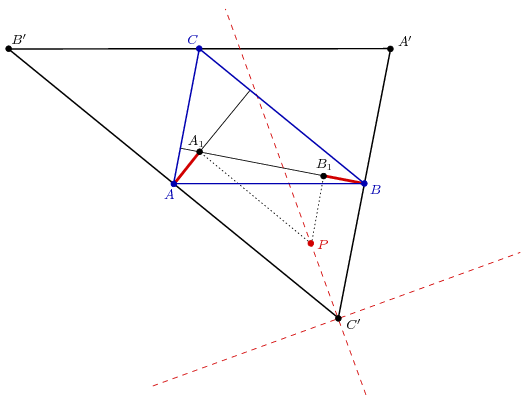
Az AA₁ szakasz merőleges BC-re és a vele párhuzamos, A-n átmenő B'C' egyenesre, továbbá PA₁-re. Ezért az AA₁ szakasz hossza azonos a P pont és a B'C' egyenes távolságával. Hasonlóképpen, BB₁ egyenlő a P pont és az A'C' egyenes távolságával. Ez a két távolság akkor egyenlő egymással, ha P a B'C' és A'C' egyenesek valamelyik szögfelezőjén van.

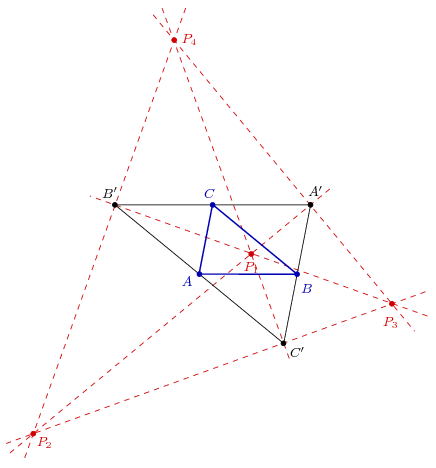
Ugyanígy, a P pontnak illeszkednie kell az A'B'C' háromszög valamelyik A'-ból, és valamelyik B-ből induló szögfelezőjére is. Összesen négy ilyen pont létezik: az A'B'C' háromszög beírt és hozzáírt közeinek középpontjai.

Statistics:

36 students sent a solution.
5 points:	Ágoston Péter, Baran Zsuzsanna, Bereczki Zoltán, Fehér Zsombor, Gyulai-Nagy Szuzina, Janzer Barnabás, Janzer Olivér, Kúsz Ágnes, Maga Balázs, Schwarcz Tamás, Szabó 789 Barnabás, Szabó 928 Attila, Williams Kada.
4 points:	Nagy-György Pál, Szalai 213 Orsolya, Zarándy Álmos.
3 points:	18 students.
2 points:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, April 2013