Problem B. 4537. (April 2013)

B. 4537. 200 line segments of unit length are placed in a 20×20 square. Prove that there exists a disc of unit diameter in the square such that it does not have a point in common with any of the line segments.

(Transcarpathian competition problem)

(5 pont)

Deadline expired on May 10, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldási ötlet: Hol (nem) lehet a körlap középpontja?

Megoldásvázlat: A körlapot nyilván elég a középpontjával megadnunk.

Olyan pontot kell találnunk, anely a négyzet belsejében van, a négyzet határától és az egységszakaszoktól is legalább 0,5 egységnyi távolságra.

A négyzet belsejében tehát egy 19×19 méretű, 19²=361 területű négyzetben kell keresnünk. Azoknak pontoknak a halmaza, amik egy konkrét egységszakasztól legfeljebb 0,5 egységnyire vannak, felbontható két félkörlemezre és egy egységnégyzetre; egy-egy ilyen tiltott halmaz területe $\frac\pi4+1$ .

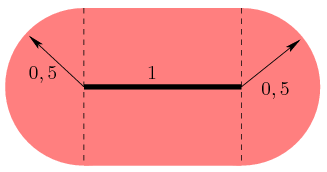
A 200 egységszakasz által tiltott terület összesen legfeljebb $200\cdot\left(\frac\pi4+1\right)\approx 357,1$ , kisebb, mint a 19×19-es négyzet területe. Ezért a tiltott halmazok nem fedhetik le a 19×19-es négyzetet; mindig létezik megfelelő középpont.

Statistics:

56 students sent a solution.

5 points: Árkos Gergely, Balogh Tamás, Baran Zsuzsanna, Bogár Blanka, Di Giovanni Márk, Emri Tamás, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Forrás Bence, Gyulai-Nagy Szuzina, Herczeg József, Janzer Barnabás, Janzer Olivér, Katona Dániel, Khayouti Sára, Leipold Péter, Leitereg Miklós, Maga Balázs, Makk László, Márton Boldizsár, Nagy Gergely, Nagy Róbert, Nagy-György Pál, Paulovics Zoltán, Petrényi Márk, Qian Lívia, Sagmeister Ádám, Sal Kristóf, Schwarcz Tamás, Simkó Irén, Somogyvári Kristóf, Szabó 157 Dániel, Szabó 524 Tímea, Szabó 789 Barnabás, Szász Dániel Soma, Szebellédi Márton, Szőke Tamás, Tossenberger Tamás, Tóth László Gábor, Vető Bálint, Williams Kada, Zilahi Tamás.

4 points: Ágoston Péter, Kulcsár Ildikó.

3 points: 5 students.

2 points: 1 student.

0 point: 5 students.

Problems in Mathematics of KöMaL, April 2013

56 students sent a solution.
5 points:	Árkos Gergely, Balogh Tamás, Baran Zsuzsanna, Bogár Blanka, Di Giovanni Márk, Emri Tamás, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Forrás Bence, Gyulai-Nagy Szuzina, Herczeg József, Janzer Barnabás, Janzer Olivér, Katona Dániel, Khayouti Sára, Leipold Péter, Leitereg Miklós, Maga Balázs, Makk László, Márton Boldizsár, Nagy Gergely, Nagy Róbert, Nagy-György Pál, Paulovics Zoltán, Petrényi Márk, Qian Lívia, Sagmeister Ádám, Sal Kristóf, Schwarcz Tamás, Simkó Irén, Somogyvári Kristóf, Szabó 157 Dániel, Szabó 524 Tímea, Szabó 789 Barnabás, Szász Dániel Soma, Szebellédi Márton, Szőke Tamás, Tossenberger Tamás, Tóth László Gábor, Vető Bálint, Williams Kada, Zilahi Tamás.
4 points:	Ágoston Péter, Kulcsár Ildikó.
3 points:	5 students.
2 points:	1 student.
0 point:	5 students.

Already signed up?
New to KöMaL?