 Problem B. 4551. (May 2013)
Problem B. 4551. (May 2013)
B. 4551. P is the point on base AB of a symmetric trapezium ABCD for which AP-BP=AC-BC. The perpendicular drawn to AB at P intersects the lines CD, AC and BD at the points Q, R and S, respectively. Let k1 be the circle that touches the lines AC and BD at points R and S, and let k2 be the circle of diameter PQ. Prove that the circles k1 and k2 touch each other.
(6 pont)
Deadline expired on June 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldási ötlet: Rajzoljuk meg a trapéz körülírt körét, továvvá az ABC és a BCD háromszögek beírt köreit. Vegyük fel a PQ és a BC egyenesek metszéspontját.
Megoldás (vázlat). Legyen k a trapéz köré írt kör, és F a k rövidebbik BC ívének felezőpontja. Legyen a PQ és BC egyenesek metszéspontja K, továbbá legyen T a k kör és a KF egyenes második, F-től különböző metszéspontja. Azt mutatjuk meg, hogy k, k1 és k2 a T pontban érintik egymást.
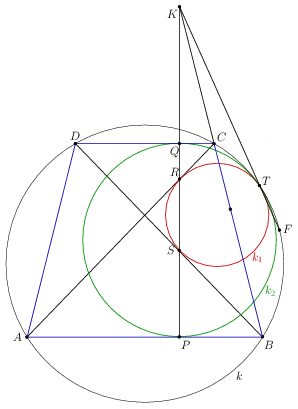
Ennek bizonyításához felhasználjuk az A. 505. feladat megoldásának ötleteit.
Legyen I, illetve J a BCD, illetve az ABC háromszögbe írt kör középpontja. Mivel AP-BP=AC-BC=BD-BC=DQ-CQ, az I és a J pont is a PQ szakaszon van.
Legyen P' a k kör C-t nem tartalmazó AB ívének felezőpontja, és Q' az ezzel szemközti CD ív felezőpontja. Mivel I és J a BCD, illetve ABC háromszög szögfelezőinek metszéspontja, I=DF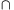 BQ'
BQ'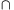 CS' és J=AF
CS' és J=AF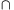 CP'
CP'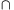 BR'. A Pascal-tételt a BCDFTQ' hatszögre felírva láthatjuk, hogy CD és TQ' az IK=PQ egyenesen metszi egymást, vagyis TQ' átmegy Q-n. Hasonlóan, az CBAFTP' hatszögre felírt Pascal-tételből kapjuk, hogy TP' átmegy P-n. A k2-höz P-ben és a k-hoz P'-ben húzott érintők párhuzamosak, és a köröknek ugyanazon az oldalán vannak. Ezért PP' átmegy a két kör külső hasonlósági pontján. Ugyanígy QQ' is átmegy a két kör külső hasonlósági pontján, a hasonlósági pont tehát T. Mivel a hasonlósági pont a k körön van, k és k2 a T-ben érinti egymást. (baloldali ábra)
BR'. A Pascal-tételt a BCDFTQ' hatszögre felírva láthatjuk, hogy CD és TQ' az IK=PQ egyenesen metszi egymást, vagyis TQ' átmegy Q-n. Hasonlóan, az CBAFTP' hatszögre felírt Pascal-tételből kapjuk, hogy TP' átmegy P-n. A k2-höz P-ben és a k-hoz P'-ben húzott érintők párhuzamosak, és a köröknek ugyanazon az oldalán vannak. Ezért PP' átmegy a két kör külső hasonlósági pontján. Ugyanígy QQ' is átmegy a két kör külső hasonlósági pontján, a hasonlósági pont tehát T. Mivel a hasonlósági pont a k körön van, k és k2 a T-ben érinti egymást. (baloldali ábra)
Legyen H1 a k és a k1 kör külső hasonlósági pontja. Azt akarjuk megmutatni, hogy H1=T.
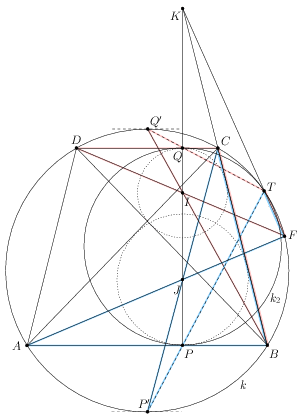
Legyen R' a k kör B-t nem tartalmazó CA ívének felezőpontja, és S' a C-t nem taralmazó DB ív felezőpontja. A BCAFTR' és CBDFTS' hatszögekre felírt Pascal-tételből kapjuk, hogy TR' átmegy R-en és TS' átmegy S, így a k1 és k külső hasonlósági pontja is T. (jobboldali ábra)
Statistics:
10 students sent a solution. 6 points: Bereczki Zoltán, Forrás Bence, Janzer Olivér, Machó Bónis, Schwarcz Tamás, Simkó Irén, Szabó 789 Barnabás, Venczel Tünde, Williams Kada. 1 point: 1 student.
Problems in Mathematics of KöMaL, May 2013
