Problem B. 4558. (September 2013)

B. 4558. The base of a regular four-sided pyramid is the unit square ABCD, its apex is E. P is a point on base edge AB, and Q is a point on lateral edge EC such that PQ is perpendicular to both AB and EC. Furthermore, AP:PB=6:1. How long are the lateral edges?

(5 pont)

Deadline expired on October 10, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen \(\displaystyle O\) az \(\displaystyle ABCD\) négyzet középpontja, \(\displaystyle R\) a \(\displaystyle DC\) szakasz \(\displaystyle C\) -hez legközelebbi hetedelőpontja, \(\displaystyle S\) pedig a \(\displaystyle Q\) pont merőleges vetülete az \(\displaystyle ABCD\) síkon.

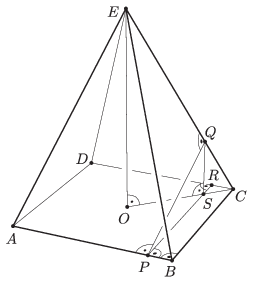
A gúla szabályosságából következően a \(\displaystyle CE\) egyenes merőleges vetülete az \(\displaystyle ABCD\) síkon a \(\displaystyle CO\) egyenes, ezért \(\displaystyle S\) rajta van a \(\displaystyle CO\) egyenesen. Mivel \(\displaystyle AP:PB=6:1\), a \(\displaystyle PR\) egyenes párhuzamos \(\displaystyle BC\)-vel, vagyis merőleges \(\displaystyle AB\)-re. \(\displaystyle PQ\) is merőleges \(\displaystyle AB\)-re, ezért \(\displaystyle AB\) merőleges a \(\displaystyle PQR\) síkra. Tehát az \(\displaystyle AB\)-re merőleges \(\displaystyle QS\) egyenes benne van a \(\displaystyle PQR\) síkban, vagyis \(\displaystyle S\) illeszkedik a \(\displaystyle PR\) egyenesre.

A \(\displaystyle CRS\) háromszög derékszögű és egyenlőszárú, ezért \(\displaystyle RS=1/7\) és \(\displaystyle CS=CR\sqrt{2}=\frac{\sqrt{2}}{7}\). A \(\displaystyle QSC\) és \(\displaystyle EOC\) háromszögek hasonlóak, mert megfelelő oldalaik párhuzamosak. A hasonlóság aránya \(\displaystyle CS:CO=\frac{\sqrt{2}}{7}:\frac{\sqrt{2}}{2}=2:7\). Ha tehát \(\displaystyle CQ=y\), akkor \(\displaystyle CE= \frac{7y}2\).

A \(\displaystyle QSC\) és \(\displaystyle QSP\) derékszögű háromszögekben Pitagorasz tétele szerint

\(\displaystyle QS^2 =CQ^2-CS^2=y^2-\frac{2}{49},\)

\(\displaystyle QP^2 =QS^2+SP^2=\left( y^2-\frac{2}{49}\right) +\left(\frac{6}{7}\right)^{2}= y^2+\frac{34}{49}.\)

Végül a \(\displaystyle PQC\) és \(\displaystyle PBC\) derékszögű háromszögek közös \(\displaystyle PC\) átfogójának négyzetét szintén Pitagorasz tétele szerint felírva kapjuk, hogy

\(\displaystyle PC^2=CQ^2+QP^2=BC^2+BP^2, \quad \text{azaz} \quad y^2+\left( y^2+\frac{34}{49}\right) =1+\frac{1}{49}. \)

Ezt az egyenletet rendezve \(\displaystyle 2y^2=\frac{16}{49}\), azaz \(\displaystyle y=\frac{\sqrt{8}}{7}\) adódik.

Tehát a gúla oldaléleinek hossza \(\displaystyle CE= \frac{7y}2=\sqrt{2}\).

Nagy Gergely (Győr, Révai M. Gimn., 11. évf.) dolgozata alapján

Statistics:

99 students sent a solution.
5 points:	72 students.
4 points:	9 students.
3 points:	5 students.
2 points:	9 students.
1 point:	3 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, September 2013