 Problem B. 4562. (October 2013)
Problem B. 4562. (October 2013)
B. 4562. In a right-angled triangle ABC, a semicircle is drawn over the leg AC, on the side where the triangle lies. A tangent is drawn to the semicircle at the point E where it intersects the hypotenuse. The tangent intersects the leg BC at point D. Prove that triangle EBD is isosceles.
(3 pont)
Deadline expired on November 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. A Thálész-tétel miatt CEA =90o. Az ACE és CBA szögek merőleges szárú hegyesszögek, így egyenlők: ACE
=90o. Az ACE és CBA szögek merőleges szárú hegyesszögek, így egyenlők: ACE =CBA
=CBA . Az ACE körben a BED
. Az ACE körben a BED érintő szárú kerületi szög, ami megegyezik az ACE szöggel. Összefoglalva,
érintő szárú kerületi szög, ami megegyezik az ACE szöggel. Összefoglalva,
DBE =CBA
=CBA =ACE
=ACE =BED
=BED .
.
Az EBD háromszög B-nél és E-nél levő szögei megegyeznek, a háromszög egyenlő szárú.
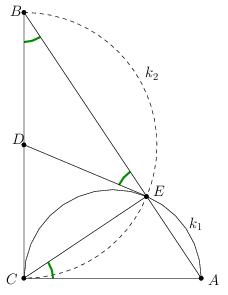
2. megoldás. Legyen k1 és k2 az AC, illetve a BC átmérőjű kör. A Thálész tétel miatt CE merőleges az AB oldalra. a Tálész-tétel megfordítása miatt a k2 kör is átmegy az E ponton. A D pontból k1-hez húzott DC és DE érintők ugyanolyan hosszúak, ezért D rajta van CE felező merőlegesén. Ugyanakkor a BC szakasz a k2 kör átmérője, így D a k2 középpontja. Tehát DB és DE a k2 kör két sugara, amik egyenlőek.
Statistics:
319 students sent a solution. 3 points: 313 students. 2 points: 2 students. 1 point: 2 students. 0 point: 2 students.
Problems in Mathematics of KöMaL, October 2013
