 Problem B. 4566. (October 2013)
Problem B. 4566. (October 2013)
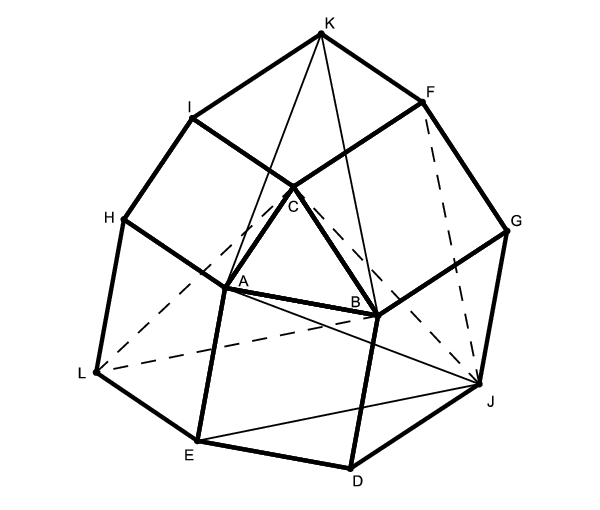
B. 4566. The squares ABDE, BCFG and CAHI are drawn over the sides of a triangle ABC, on the outside. The triangles DBG, FCI and HAE are completed to form the parallelograms DBGJ, FCIK and HAEL. Prove that .
Suggested by Sz. Miklós, Herceghalom
(5 pont)
Deadline expired on November 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Egy \(\displaystyle \overrightarrow{v}\) vektor \(\displaystyle 90^{\circ}\)-kal való elforgatottját jelölje \(\displaystyle \overrightarrow{v}'\), egy \(\displaystyle P\) pontét pedig \(\displaystyle P'\).
Ekkor
\(\displaystyle \overrightarrow{AK}=\overrightarrow{AC}+\overrightarrow{CI}+\overrightarrow{IK}= -\overrightarrow{CA}+\overrightarrow{CA}'+\overrightarrow{CF}=-\overrightarrow{CA}+\overrightarrow{CA}'+\overrightarrow{BC}',\)
amiből
\(\displaystyle \overrightarrow{AK}'=(-\overrightarrow{CA}+\overrightarrow{CA}'+\overrightarrow{BC}')'= (-\overrightarrow{CA})'+(\overrightarrow{CA}')'+(\overrightarrow{BC}')'= -\overrightarrow{CA}'-\overrightarrow{CA}-\overrightarrow{BC}.\)
Felírható, hogy \(\displaystyle \overrightarrow{AJ}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DJ}= \overrightarrow{AB}+\overrightarrow{AB}'+\overrightarrow{BC}'\).
Tudjuk, hogy \(\displaystyle \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{0}\), és így \(\displaystyle (\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA})' =\overrightarrow{AB}'+\overrightarrow{BC}'+\overrightarrow{CA}'=\overrightarrow{0}'=\overrightarrow{0}\), így \(\displaystyle \overrightarrow{AB}'+\overrightarrow{BC}'=-\overrightarrow{CA}'\) és \(\displaystyle \overrightarrow{AB}=-\overrightarrow{BC} -\overrightarrow{CA}\), tehát \(\displaystyle \overrightarrow{AK}'=\overrightarrow{AJ}\). Tehát a \(\displaystyle K\) pont \(\displaystyle A\) körüli \(\displaystyle -90^{\circ}\)-os elforgatottja a \(\displaystyle J\) pont, a \(\displaystyle B\) pont elforgatottja az \(\displaystyle E\) pont, ezért az \(\displaystyle AKB\triangle\) elforgatottja az \(\displaystyle AJE\triangle\). Emiatt \(\displaystyle AKB\sphericalangle=AJE\sphericalangle\).
Hasonlóan belátható, hogy a \(\displaystyle BLC\triangle\) \(\displaystyle C\) körüli \(\displaystyle +90^{\circ}\)-os elforgatottja az \(\displaystyle FJC\triangle\), ami miatt \(\displaystyle BLC\sphericalangle=FJC\sphericalangle\).
Tehát \(\displaystyle AKB\sphericalangle+BLC\sphericalangle+CJA\sphericalangle=AJE\sphericalangle+FJC\sphericalangle+CJA\sphericalangle=FJE\sphericalangle\). Erről kéne belátni, hogy \(\displaystyle 90^{\circ}\). Mivel \(\displaystyle \overrightarrow{JE}=\overrightarrow{JD}+\overrightarrow{DE}\), így \(\displaystyle \overrightarrow{JE}'=(\overrightarrow{JD}+\overrightarrow{DE})'=(\overrightarrow{GB}+\overrightarrow{DE})'= \overrightarrow{GB}'+\overrightarrow{DE}'=\overrightarrow{GF}+\overrightarrow{DB}=\overrightarrow{GF}+ \overrightarrow{JG}=\overrightarrow{JF}\). Tehát az \(\displaystyle F\) pont az \(\displaystyle E\) pont \(\displaystyle J\) körüli \(\displaystyle -90^{\circ}\)-os elforgatottja. Ezzel beláttuk, hogy \(\displaystyle FJE\sphericalangle=90^{\circ}\), a bizonyítást befejeztük.
Statistics:
98 students sent a solution. 5 points: Balogh Tamás, Barabás Ábel, Di Giovanni Márk, Egyházi Anna, Fekete Panna, Geng Máté, Kabos Eszter, Kocsis Júlia, Kúsz Ágnes, Lajkó Kálmán, Leipold Péter, Machó Bónis, Maga Balázs, Nagy-György Pál, Nagy-György Zoltán, Schwarcz Tamás, Varga Rudolf, Viharos Loránd Ottó, Williams Kada. 4 points: 57 students. 3 points: 9 students. 2 points: 3 students. 1 point: 6 students. 0 point: 2 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, October 2013
