Problem B. 4572. (November 2013)

B. 4572. Solve the following simultaneous inequalities on the set of pairs of integers: 11>2a-b, 25>2b-a, 42<3b-a and 46<2a+b.

(3 pont)

Deadline expired on December 10, 2013.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Mivel mindenhol egész számokról van szó, az egyenlőtlenségeket átírhatjuk úgy, hogy az egyenlőséget is megengedjük; ehhez a megfelelő konstanst kell 1-gyel növelnünk vagy csökkentenünk, az egyenlőtlenség irányától függően:

10 $\ge$ 2a-b,

(1)

24 $\ge$ 2b-a,

(2)

43 $\le$ 3b-a,

(3)

47 $\le$ 2a+b.

(4)

Az (1) és (2) alapján

3a=2(2a-b)+(2b-a) $\le$ 2^.10+24=44,

a $\le$ 14.

(5)

Hasonlóan,

3b=(2a-b)+2(2b-a) $\le$ 10+2^.24=58,

b $\le$ 19.

(6)

Az (5)-öt és (6)-ot beírva (4)-be,

47 $\le$ 2a+b $\le$ 2^.14+19=47.

Ez csak úgy lehetséges, ha a=14 és b=19.

Behelyettesítéssel ellenőrizük, hogy a (14,19) számpárra valóban teljesülnek a kívánt egyenlőtlenségek:

2a-b=2^.14-19=9<11,

2b-a=2^.19-14=24<25,

3b-a=3^.19-14=43>42,

végül

2a+b=2^.14+19=47>46.

Az egyenlőtlenségrendszer egyetlen megoldása tehát a (14,19) pár.

2. (grafikus) megoldás, vázlat:

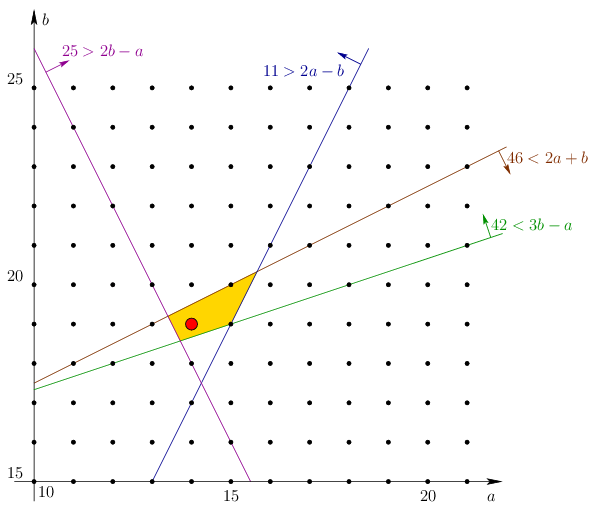
Statistics:

228 students sent a solution.

3 points: 166 students.

2 points: 13 students.

1 point: 11 students.

0 point: 28 students.

Unfair, not evaluated: 10 solutionss.

Problems in Mathematics of KöMaL, November 2013

228 students sent a solution.
3 points:	166 students.
2 points:	13 students.
1 point:	11 students.
0 point:	28 students.
Unfair, not evaluated:	10 solutionss.

Already signed up?
New to KöMaL?