 Problem B. 4573. (November 2013)
Problem B. 4573. (November 2013)
B. 4573. Prove that among any seven vertices of a regular 27-sided polygon there are four that form a trapezium.
Competition problem from Germany, 2012
(6 pont)
Deadline expired on December 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. Húzzuk meg a hét kiválasztott csúcsot összekötő, összesen szakaszt. A szabályos 27-szög csúcsai között csak 13-féle távolság fordulhat elő, ezért a szakaszok között biztosan vannak egyenlő hosszúságúak.
Ha a hét pont között van négy különböző, A, B. C és D, amire AB=CD, akkor ezek mindenképpen trapézt határoznak meg (1. és 2. ábra). Két szakasz ezért csak úgy lehet egyenlő, ha az egyik végpontjuk közös.
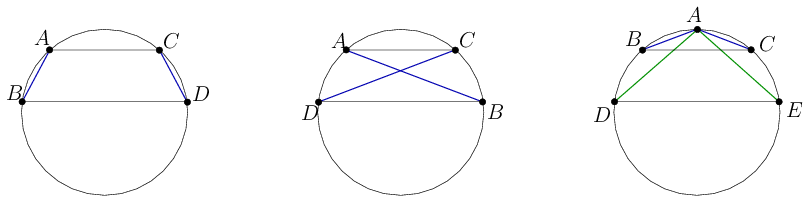
Mivel 21 szakaszunk van, és legfeljebb csak 13-féle hosszúság, legalább 8 különböző olyan szakaszpár található, amely egyforma hosszúságú szakaszokból áll. A 7 csúcs között ezért van olyan A csúcs, ami legalább két szakaszpár esetén a közös végpont, azaz vannak olyan B,C,D,E csúcsok a többi hat között, amikre AB=AC és AC=AD. Ekkor viszont B,C,D,E trapézt határoz meg (3. ábra).
Statistics:
61 students sent a solution. 6 points: Ágoston Péter, Andó Angelika, Baran Zsuzsanna, Cseh Kristóf, Csernák Tamás, Fonyó Viktória, Gyulai-Nagy Szuzina, Lajkó Kálmán, Lajos Hanka, Leipold Péter, Leitereg Miklós, Maga Balázs, Öreg Botond, Sándor Krisztián, Szabó 789 Barnabás, Szegedi Áron, Talyigás Gergely, Williams Kada. 5 points: Babik Bálint, Badacsonyi István András, Csépai András, Dinev Georgi, Geng Máté, Kalló Kristóf, Khayouti Sára, Kocsis Júlia, Kovács 972 Márton, Nagy Simon József, Temesi András, Várkonyi Dorka, Viharos Loránd Ottó. 2 points: 13 students. 1 point: 3 students. 0 point: 12 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, November 2013
