 |
A B. 4583. feladat (2013. december) |
B. 4583. Az AB szakaszon adottak a D és E pontok. Az AD, DB, AE és EB szakaszokra ugyanabban a félsíkban emelt szabályos háromszögek harmadik csúcsai rendre F, G, H és I. Igazoljuk, hogy ha az FI és GH egyenesek nem párhuzamosak, akkor metszéspontjuk rajta van az AB egyenesen.
Javasolta: Miklós Szilárd (Herceghalom)
(3 pont)
A beküldési határidő 2014. január 10-én LEJÁRT.
1. megoldás (vázlat). Ha fecseréljük a D,F,G pontok szerepét az E,I,H pontokkal, az állítás önmagába megy át. Ezért az általánosság sérülése nélkül feltehetjük, hogy AD<AE. Legyen a=AD, b=DE, c=EB.
Ha a=c, akkor az FI és a GH egyenes is párhuzamos AB-vel, és kész vagyunk. A továbbiakban feltételezzük, hogy a c. Legyen M=AB
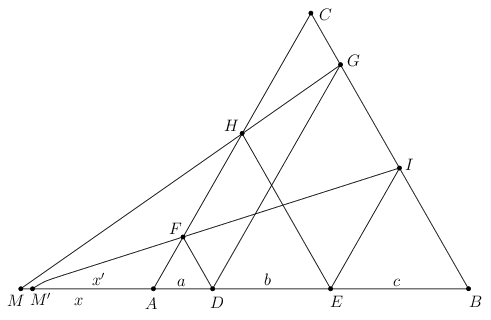
c. Legyen M=AB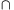 GH és M'=AB
GH és M'=AB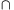 FI. Azt akarjuk igazlni, hogy M=M'. Ismét az állítás szimmetriája miatt (
FI. Azt akarjuk igazlni, hogy M=M'. Ismét az állítás szimmetriája miatt (,
,
,
,
) feltehetjük, hogy a<c; ekkor M és M' is a BA félegyenes A-n túli meghosszabbításán van, és a megoldáshoz elég azt ellenőrizni, hogy AM=AM'. Legyen x=AM és x'=AM'.
A párhuzamos szelőt tételét alkalmazzuk az MAB és az MHG egyeneseket párhuzamosan metsző AH és EI, illetve EH és BG szelőire:
x(x+a+b+c)=(x+a+b)(x+a)
Hasonlóan, az M'AB és M'FI egyenesekre felírva a párhuzamos szelők tételét,
x'(x'+a+b+c)=(x'+a)(x'+a+b)
Tehát x'=x és így M=M'; az GH és FI egyenesek az AB egyenes M pontjában metszik egymást.
2. megoldás (vázlat). Írjuk fel a Menelaosz-tételt az ABC háromszögre kétféleképpen, a GHM és az FIM' egyenesre is, Az előző megoldás jeöléseivel
illetve
Láthatjuk, hogy , amiből következi, hogy M'=M.
3. megoldás (vázlat). A megoldáshoz projektív geometriai eszközöket, pontnégyesek kettősviszonyának jól ismert tulajdonságait használjuk fel.
Legyen C=AF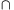 BI. A párhuzamos vetítések és az (XYUV)=(YXVU) azonosság miatt
BI. A párhuzamos vetítések és az (XYUV)=(YXVU) azonosság miatt
(ACFH)=(ABDE)=(CBGI)=(BCIG).
Az (A,C,F,G) és a (B,C,I,G) pontnégyeseknek vagy közös pontja (a C pont), ezért a két pontnégyes perspektív: az AB, FI és HG egyenes (a projektív síkon) egy ponton megy át.
Statisztika:
131 dolgozat érkezett. 3 pontot kapott: 114 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 6 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2013. decemberi matematika feladatai

