Problem B. 4584. (December 2013)

B. 4584. A line is drawn through each of two opposite vertices of a parallelogram such that each line intersects the extensions of the sides of the parallelogram at two points. Prove that the four points of intersection form a trapezium.

Suggested by G. Moussong, Budapest

(4 pont)

Deadline expired on January 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Betűzzük a paralelogrammát és a metszéspontokat az ábra szerint. Azt akarjuk megmutatni, hogy az PR és az SQ szakasz párhuzamos egymással. Mivel AB||CD és AD||BC, a következők ekvivalensek:

(a) az PR és az SQ szakasz párhuzamos egymással;

(b) a BRB és DQS háromszögek hasonlók;

(c) .

A (c) állítást fogjuk igazolni.

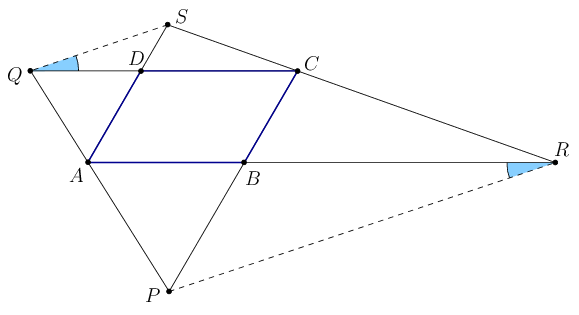
A PBA és ADQ háromszögek hasonlók, mert megfelelő oldalaik párhuzamosak, ezért

(1)

A CBR és SDC háromszögek is hasonlók, és

(2)

A paralelogramma szemközti oldalai egyenlők, így

(3).

Az (1), (2) és (3) szorzata a (c) állítás.

2. megoldás. Alkalmazzuk a Papposz-tételt az A,P,Q és C,S,R ponthármasokra.

Statistics:

133 students sent a solution.
4 points:	90 students.
3 points:	33 students.
2 points:	4 students.
1 point:	2 students.
0 point:	4 students.

Problems in Mathematics of KöMaL, December 2013