Problem B. 4586. (December 2013)

B. 4586. K, L and M are points of sides AB, AC and BC of triangle ABC, respectively. KL is parallel to BC, KL=LC, and $LMB\sphericalangle = BAC\sphericalangle$ . Prove that LM=AK.

(Kvant)

(4 pont)

Deadline expired on January 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Mivel $\displaystyle KL||BC$ és $\displaystyle KL=LC$, láthatjuk, hogy $\displaystyle KCB\angle = CKL\angle = LCK\angle$, és így $\displaystyle CK$ az $\displaystyle ACB\angle$ felezője.

Legyen $\displaystyle N$ az a pont az $\displaystyle AB$ egyenesen, amire $\displaystyle KN$ párhuzamos $\displaystyle LM$-mel. Ekkor tehát $\displaystyle KL||MN$ és $\displaystyle KN||LM$, vagyis a $\displaystyle KLMN$ négszög paralelogramma. Mivel $\displaystyle CNK\angle=CML\angle=180^\circ-LMB\angle=180^\circ-KAC\angle$, az $\displaystyle AKNC$ négyszög húrnégyszög.

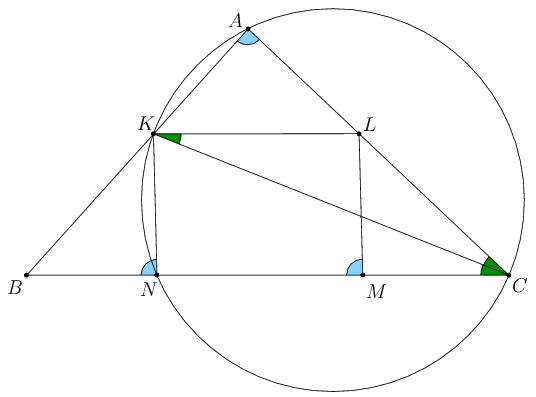
Mivel $\displaystyle CK$ az $\displaystyle ACN$ szög felezője, az $\displaystyle AKNC$ négyszög köré írt körön az $\displaystyle AK$ és $\displaystyle KN$ ívek ugyanakkora kerületi szöghöz tartoznak, így $\displaystyle AK=KN$. Mivel pedig $\displaystyle KLMN$ paralelogramma, $\displaystyle KN=LM$. Tehát,

$\displaystyle AK = KN = LM. $

Statistics:

144 students sent a solution.

4 points: 125 students.

3 points: 14 students.

0 point: 5 students.

Problems in Mathematics of KöMaL, December 2013

144 students sent a solution.
4 points:	125 students.
3 points:	14 students.
0 point:	5 students.

Already signed up?
New to KöMaL?