 Problem B. 4587. (December 2013)
Problem B. 4587. (December 2013)
B. 4587. Solve the equation .
(3 pont)
Deadline expired on January 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mint jól ismert,
ezért megoldása az egyenletnek.
Az egyenlet baloldala
Ha x 0, akkor ez nempozitív, így az egyenlet nem teljesülhet. A (0,
0, akkor ez nempozitív, így az egyenlet nem teljesülhet. A (0,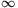 ) félegyenesen pedig a
) félegyenesen pedig a kifejezés két pozitív, szigorúan növő függvény szorzata, ezért maga is szigorúan monoton nő. Így legfeljebb egy pozitív megoldás létezhet, amit már meg is találtunk.
Az egyenletnek egy valós megoldása van: .
Statistics:
207 students sent a solution. 3 points: 67 students. 2 points: 96 students. 1 point: 30 students. 0 point: 9 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, December 2013
