Problem B. 4588. (December 2013)

B. 4588. The point D lies in the interior of a triangle ABC. Lines CD, AD and BD intersect sides AB, BC and CA at the points E, F and G, respectively. The intersection of lines EG and AF is H, and that of lines EF and BG is I. Show that the lines AB, FG and HI are concurrent.

Suggested by Sz. Miklós, Herceghalom

(5 pont)

Deadline expired on January 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Alkalmazzuk a Desargues-tétel megfordítását az AGH és BFI háromszögekre. Mivel a megfelelő oldalpárok metszéspontjai (C=AG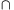 $\cap$ BF, D=AH 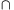$\cap$ BI, és E=GH 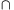$\cap$ FI) egy egyenesen vannak, a megfelelő csúcsokat összekötő egyenesek, nevezetesen AB, GF és HI egy ponton mennek át, vagy párhuzamosak.

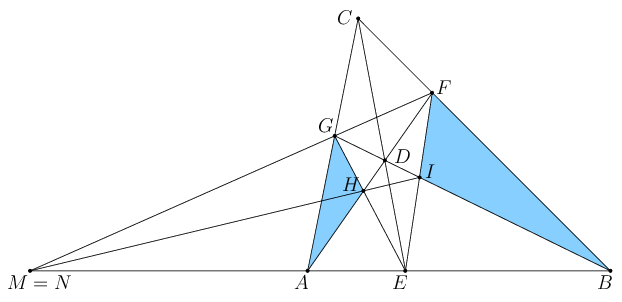
2. megoldás. Legyen AB metszéspontja a GF és a HI egyenessel M, illetve N. Azt akarjuk igazolni, hogy M=N; ehhez elég azt ellenőrizni, hogy (előjeles távolságokkal) $\frac{AM}{MB}=\frac{AN}{NB}$ . (Ha GF vagy HI párhuzamos AB-vel, akkor $\frac{AM}{MB}=1$ , illetve $\frac{AN}{NB}=1$ .)

Írjuk fel a Ceva-tételt és a Menelaosz-tételt a következő hatféle módon.

Menelaosz-tétel az ABD háromszögre és az FGM egyenesre: $\frac{AM}{MB} \cdot \frac{BG}{GD} \cdot \frac{DF}{FA} = -1$

Menelaosz-tétel az ABD háromszögre és a HIN egyenesre: $\frac{BN}{NA} \cdot \frac{AH}{HD} \cdot \frac{DI}{IB} = -1$

Ceva-tétel az ADG háromszögre és az E pontra: $\frac{HD}{AH} \cdot \frac{BG}{DB} \cdot \frac{CA}{GC} = 1$

Menelaosz-tétel az ADG háromszögre és a BFC egyenesre: $\frac{DB}{BG} \cdot \frac{GC}{CA} \cdot \frac{AF}{FD} = -1$

Ceva-tétel a BFD háromszögre és az E pontra: $\frac{IB}{DI} \cdot \frac{CF}{BC} \cdot \frac{AD}{FA} = 1$

Menelaosz-tétel a BFD háromszögre és az AGC egyenesre: $\frac{BC}{CF} \cdot \frac{FA}{AD} \cdot \frac{DG}{GB} = -1$

A fenti 6 képlet szorzata $\frac{AM}{MB} \cdot \frac{BN}{NA} = 1$ . Tehát $\frac{AM}{MB}=\frac{AN}{NB}$ , és így M=N. Ezzel az állítást igazoltuk.

Statistics:

35 students sent a solution.

5 points: Andó Angelika, Bereczki Zoltán, Cseh Kristóf, Csépai András, Di Giovanni Márk, Fekete Panna, Forrás Bence, Geng Máté, Gyulai-Nagy Szuzina, Hansel Soma, Horeftos Leon, Kabos Eszter, Kovács 972 Márton, Kúsz Ágnes, Lajkó Kálmán, Maga Balázs, Nagy Gergely, Nagy Odett, Nagy-György Pál, Petrényi Márk, Radó Hanna, Schwarcz Tamás, Simkó Irén, Szegi Bogát, Vághy Mihály, Vágó Ákos, Williams Kada.

4 points: Herczeg József, Mócsy Miklós, Szabó 789 Barnabás, Szebellédi Márton, Tulassay Zsolt.

3 points: 2 students.

1 point: 1 student.

Problems in Mathematics of KöMaL, December 2013

35 students sent a solution.
5 points:	Andó Angelika, Bereczki Zoltán, Cseh Kristóf, Csépai András, Di Giovanni Márk, Fekete Panna, Forrás Bence, Geng Máté, Gyulai-Nagy Szuzina, Hansel Soma, Horeftos Leon, Kabos Eszter, Kovács 972 Márton, Kúsz Ágnes, Lajkó Kálmán, Maga Balázs, Nagy Gergely, Nagy Odett, Nagy-György Pál, Petrényi Márk, Radó Hanna, Schwarcz Tamás, Simkó Irén, Szegi Bogát, Vághy Mihály, Vágó Ákos, Williams Kada.
4 points:	Herczeg József, Mócsy Miklós, Szabó 789 Barnabás, Szebellédi Márton, Tulassay Zsolt.
3 points:	2 students.
1 point:	1 student.

Already signed up?
New to KöMaL?