Problem B. 4590. (December 2013)

B. 4590. Two points and a circle k all lie on the surface of the same sphere. The circle passes through exactly one of the two points. How many circles are there on the sphere that pass through both points and are tangent to the circle k?

(5 pont)

Deadline expired on January 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Megmutatjuk, hogy pontosan egy ilyen kör létezik.

Jelöljük T-vel a k-re illeszkedő előírt pontot, és P-vel a másikat. A k síkja legyen S, a T-ben húzott érintője t. Vegyük észre, hogy az t egyenes T-től különböző pontjai a gömbön kívül vannak, ezért t a gömböt is érinti.

Először megmutatjuk, hogy a kívánt körvonal mindig létezik. Legyen S₁ a P pontra és a T egyenesre illeszkedő sík, és legyen a k₁ kör a gömb és az S₁ sík metszete. Mivel P és T illeszkedik a gömbre és az S₁ síkra is, a k₁ kör átmegy P-n és T-n. Ebből azt is láthatjuk, hogy a metszet nem fajulhat egy ponttá.

A t egyenes a k₁ kör síkjában van, és az egyetlen közös pontjuk T; ezért a t egyenes a T pontban érinti k₁-et. A T pontban k és k₁ is érinti T-t, a két kör tehát egymást is érinti.

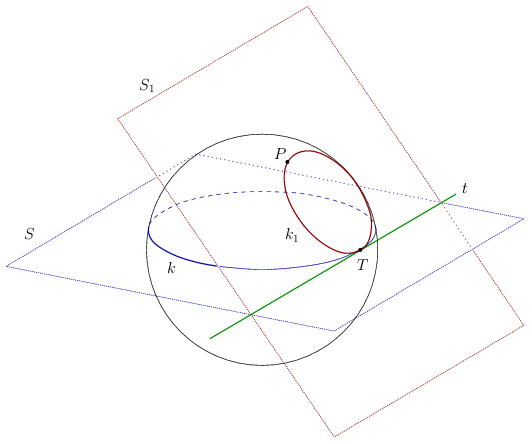
Az egyértelműség bizonyításához a fenti lépéseket fordítjuk meg. Tegyük fel, hogy k₁ olyan kör, ami átmegy P-n és T-n, továbbá érinti k-t. A k és a k₁ kör különböző, mert k₁ átmegy P-n, k viszont nem. Mivel két különböző, egymást érintő körnek csak egyetlen közös pontja lehet, az érintési pont T. A T pontban k₁ és t is érinti k-t, következésképpen t érinti k₁-et. Ekkor viszont t benne van k₁ síkjában, avagy k₁ benne van a P-re és t-re illeszkedő síkban. Mivel t nem megy át P-n, ez a sík, és vele együtt a k₁ kör is egyértelmű.

Statistics:

69 students sent a solution.
5 points:	Ágoston Péter, Baran Zsuzsanna, Berta Dénes, Csabai Bence, Csernák Tamás, Di Giovanni Márk, Dinev Georgi, Fekete Panna, Fonyó Viktória, Forrás Bence, Frank György, Gyulai-Nagy Szuzina, Hansel Soma, Herczeg József, Jenei Dániel Gábor, Kabos Eszter, Kátay Tamás, Katona Dániel, Kovács Balázs Marcell, Kúsz Ágnes, Lajkó Kálmán, Leitereg Miklós, Maga Balázs, Nagy Gergely, Nagy Kartal, Nagy-György Pál, Nemes György, Öreg Botond, Paulovics Zoltán, Petrényi Márk, Schrettner Bálint, Schulcz Ferenc, Schwarcz Tamás, Szabó 789 Barnabás, Szász Dániel Soma, Tóth Viktor, Tulassay Zsolt, Vető Bálint, Williams Kada.
4 points:	Cseh Kristóf, Csitári Nóra, Glattfelder Hanna, Leipold Péter, Németh 777 Róbert, Sal Kristóf, Szakács Lili Kata, Thamó Emese.
3 points:	7 students.
2 points:	1 student.
1 point:	5 students.
0 point:	7 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, December 2013