 Problem B. 4592. (January 2014)
Problem B. 4592. (January 2014)
B. 4592. What may be the number of people in a company in which every member has exactly three acquaintances, and any two people have an acquaintance in common exactly if the two of them do not know each other?
(5 pont)
Deadline expired on February 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. Az ismeretségi rendszert szemléltessük egy irányítatlan gráffal. Mivel most minden csúcs fokszáma 3, így a csoport páros. Bármely két ember vagy ismeri egymást, vagy van közös ismerősük. Tehát ha kiválasztunk valakit, akkor annak 3 ismerőse van, és ennek a 3 ismerősnek van fejenként még 2 másik ismerőse (akik egymástól nem feltétlenül különböznek). Ez legfeljebb \(\displaystyle 1+3+6=10\) főt jelent. Tehát a létszám 2, 4, 6, 8 vagy 10 lehet.
Ebből a 2 és a 4 nem lehetséges, a 6, a 8 és a 10 pedig igen:
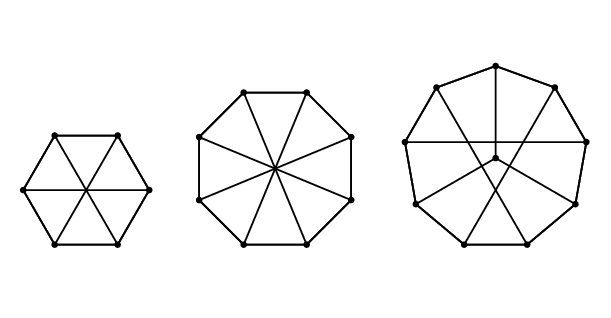
Statistics:
157 students sent a solution. 5 points: 74 students. 4 points: 7 students. 3 points: 6 students. 2 points: 10 students. 1 point: 52 students. 0 point: 6 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, January 2014
