Problem B. 4598. (January 2014)

B. 4598. The diagonals of a cyclic quadrilateral ABCD intersect at E, the midpoints of sides AB and CD are K and M, and the perpendicular projections of point E on the sides BC and AD are L and N, respectively. Prove that the lines KM and LN are perpendicular to each other.

(Kvant)

(5 pont)

Deadline expired on February 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen az \(\displaystyle AE\) szakasz felezőpontja \(\displaystyle F\), a \(\displaystyle BE\) szakaszé pedig \(\displaystyle G\). Az \(\displaystyle ANE\) és \(\displaystyle BLE\) háromszögek derékszögűek, ezért az \(\displaystyle AE\), illetve \(\displaystyle EB\) átmérőjű Thalész-körök ezen háromszögek köré írható körei, középpontjaik \(\displaystyle F\) és \(\displaystyle G\). Emiatt \(\displaystyle AF=FE=FN\) és \(\displaystyle BG=GE=GL\).

Az \(\displaystyle ABCD\) húrnégyszög, ezért \(\displaystyle CBD\sphericalangle =CAD\measuredangle =\varphi\), mivel a \(\displaystyle CD\) ívhez tartozó kerületi szögek. Így az előbbi derékszögű háromszögekben a középponti és kerületi szögek összefüggését felhasználva \(\displaystyle NFE\sphericalangle=2\varphi\) és \(\displaystyle EGL\sphericalangle =2\varphi\).

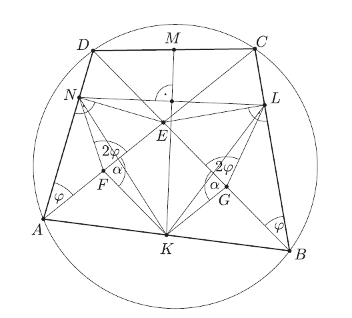
Az \(\displaystyle ABE\) háromszögben \(\displaystyle KF\) és \(\displaystyle KG\) középvonalak, ezért az \(\displaystyle EFKG\) négyszög paralelogramma, így szemközti szögei egyenlők: \(\displaystyle EFK\sphericalangle =KGE\sphericalangle =\alpha\).

Mivel \(\displaystyle KG=FE=FN\) és \(\displaystyle KF=GE=GL\), azért \(\displaystyle NFK\triangle \cong KGL\triangle\), mivel két oldaluk és a közbezárt szög megegyezik. Tehát \(\displaystyle NK=KL\), vagyis az \(\displaystyle LNK\) háromszög egyenlő szárú, így \(\displaystyle NL\) alapjának felezőmerőlegese átmegy a \(\displaystyle K\) ponton.

Hasonló gondolatmenettel belátható, hogy az \(\displaystyle LNM\) háromszög is egyenlő szárú, és \(\displaystyle LN\) alapjának felezőmerőlegese átmegy az \(\displaystyle M\) ponton.

Beláttuk, hogy az \(\displaystyle LN\) szakasz felezőmerőlegese átmegy \(\displaystyle K\) és \(\displaystyle M\) pontokon is, vagyis \(\displaystyle KM\) valóban merőleges az \(\displaystyle NL\) szakaszra, sőt még felezi is.

Az ábrán \(\displaystyle CBD\sphericalangle\) és \(\displaystyle CAD\sphericalangle\) hegyesszögek. Ilyenkor \(\displaystyle L\) és \(\displaystyle N\) pontok a \(\displaystyle BC\) és \(\displaystyle AD\) szakaszok belső pontjai. Ha a két szög tompaszög lenne, akkor ezek a pontok az \(\displaystyle AD\) és \(\displaystyle BC\) szakaszok meghosszabbításán keletkező külső pontok lesznek, de a gondolatmenet változatlanul működik.

Ha a két szög derékszög, akkor a pontok a \(\displaystyle CD\) szakasz Thalész-körén lesznek rajta, azaz \(\displaystyle L\) és \(\displaystyle N\) megegyezik az \(\displaystyle A\) és \(\displaystyle B\) pontokkal. Ekkor \(\displaystyle KM\) egyenes a Thalész-kör átmérője, ami áthalad \(\displaystyle LN\), azaz \(\displaystyle AB\) húr felezőpontján, ezért éppen a húr felezőmerőlegese.

Győrfi-Bátor András (Kaposvár, Táncsics Mihály Gimn., 12. évf.) dolgozata alapján

Statistics:

38 students sent a solution.
5 points:	Ágoston Péter, Andi Gabriel Brojbeanu, Andó Angelika, Baran Zsuzsanna, Bereczki Zoltán, Boguszlavszkij Gergely, Bus Tamás, Cseh Kristóf, Csépai András, Fekete Panna, Fonyó Viktória, Forrás Bence, Geng Máté, Győrfi-Bátori András, Gyulai-Nagy Szuzina, Kabos Eszter, Kocsis Júlia, Kovács 972 Márton, Kúsz Ágnes, Leitereg Miklós, Lengyel Ádám, Maga Balázs, Nagy Gergely, Nagy-György Pál, Petrényi Márk, Sal Kristóf, Sándor Krisztián, Sárosdi Zsombor, Schwarcz Tamás, Sütő Máté, Szőke Tamás, Williams Kada.
4 points:	Dinev Georgi, Vető Bálint, Vu Mai Phuong, Zsók Bianka.
3 points:	2 students.

Problems in Mathematics of KöMaL, January 2014