 Problem B. 4608. (February 2014)
Problem B. 4608. (February 2014)
B. 4608. The perpendicular projections of the centroid S of a triangle ABC on sides BC, AC and AB are A1, B1 and C1, respectively. Prove that (with conventional notations) .
(4 pont)
Deadline expired on March 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelölje a háromszög területét \(\displaystyle T\), az \(\displaystyle A\) csúcsból induló magasságát \(\displaystyle m_a\), a \(\displaystyle BC\) oldal felezőpontja pedig legyen \(\displaystyle F\).
Nagyítsuk az \(\displaystyle \overrightarrow{SA_1}\) vektort \(\displaystyle F\)-ből háromszorosára. Mivel a súlypont harmadolja a súlyvonalat, ezért \(\displaystyle S\) képe \(\displaystyle A\) lesz, a merőlegesség miatt pedig \(\displaystyle A_1\) képe az \(\displaystyle ABC\) háromszög \(\displaystyle A\) csúcsából induló magasságának a talppontja (1. ábra). Vagyis \(\displaystyle 3|\overrightarrow{SA_1}|=m_a\). Ezért a \(\displaystyle 2T=am_a\) képletet felhasználva kapjuk, hogy
\(\displaystyle a^2\overrightarrow{SA_1}= a\frac{2T}{3|\overrightarrow{SA_1}|}\overrightarrow{SA_1}= \frac{2T}{3}a\frac{\overrightarrow{SA_1}}{|\overrightarrow{SA_1}|}. \)
Ugyanezeket az átalakításokat a másik két tagra is elvégezve a bizonyítandó állítás
\(\displaystyle \tag{1} \frac{2T}{3} \left(a\frac{\overrightarrow{SA_1}}{|\overrightarrow{SA_1}|} +b\frac{\overrightarrow{SB_1}}{|\overrightarrow{SB_1}|} +c\frac{\overrightarrow{SC_1}}{|\overrightarrow{SC_1}|}\right) =\mathbf{0}.\)
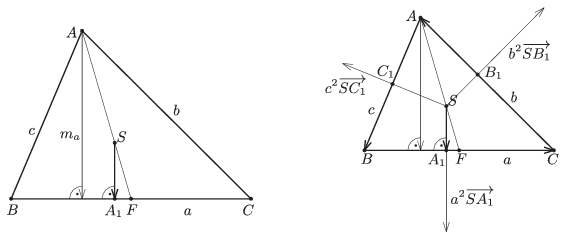
1. ábra 2. ábra
Az \(\displaystyle a\frac{\overrightarrow{SA_1}}{|\overrightarrow{SA_1}|}\) vektor hossza \(\displaystyle a\), vagyis megegyezik a háromszög \(\displaystyle BC\) oldalának hosszával, iránya pedig a \(\displaystyle \overrightarrow{BC}\) vektor \(\displaystyle -90^{\circ}\)-os elforgatottja, és hasonló igaz a zárójelben szereplő másik két vektorra is (2. ábra). Ezért - egy tetszőleges \(\displaystyle \mathbf{v}\) vektor \(\displaystyle -90^{\circ}\)-os elforgatottját \(\displaystyle \mathbf{v}'\)-vel jelölve -
\(\displaystyle a\frac{\overrightarrow{SA_1}}{|\overrightarrow{SA_1}|}+ b\frac{\overrightarrow{SB_1}}{|\overrightarrow{SB_1}|} +c\frac{\overrightarrow{SC_1}}{|\overrightarrow{SC_1}|}=\overrightarrow{BC}'+ \overrightarrow{CA}'+\overrightarrow{AB}'. \)
Vektorok adott szögű elforgatottjainak összege megegyezik az összegük adott szögű elforgatottjával, ezért
\(\displaystyle \overrightarrow{BC}'+\overrightarrow{CA}'+\overrightarrow{AB}'= \Big(\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}\Big)^{\!\prime} = \mathbf{0}'=\mathbf{0}, \)
vagyis az (1) egyenlőség teljesül.
Ezzel a feladat állítását igazoltuk.
Öreg Botond (Budapesti Fazekas M. Ált. Isk. és Gimn., 11. évf.) dolgozata alapján
Statistics:
41 students sent a solution. 4 points: Andi Gabriel Brojbeanu, Baran Zsuzsanna, Bereczki Zoltán, Cseh Kristóf, Csépai András, Di Giovanni Márk, Dinev Georgi, Forrás Bence, Geng Máté, Gyulai-Nagy Szuzina, Kabos Eszter, Kocsis Júlia, Kovács 972 Márton, Kúsz Ágnes, Le Minh 816 Hoang, Maga Balázs, Nemes György, Öreg Botond, Páli Petra, Petrényi Márk, Schwarcz Tamás, Simkó Irén, Szebellédi Márton, Tóth Viktor, Vágó Ákos, Varga 123 Péter, Vető Bálint, Vu Mai Phuong, Wiandt Péter, Williams Kada. 3 points: Kátay Tamás, Porupsánszki István. 1 point: 1 student. 0 point: 8 students.
Problems in Mathematics of KöMaL, February 2014
