Problem B. 4610. (February 2014)

B. 4610. K is the centre of the circumscribed circle of an acute triangle ABC. O is the centre of the inscribed circle, and M is the orthocentre. Is it possible for the points O, K and M to be the vertices of an isosceles triangle?

(Kvant)

(6 pont)

Deadline expired on March 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

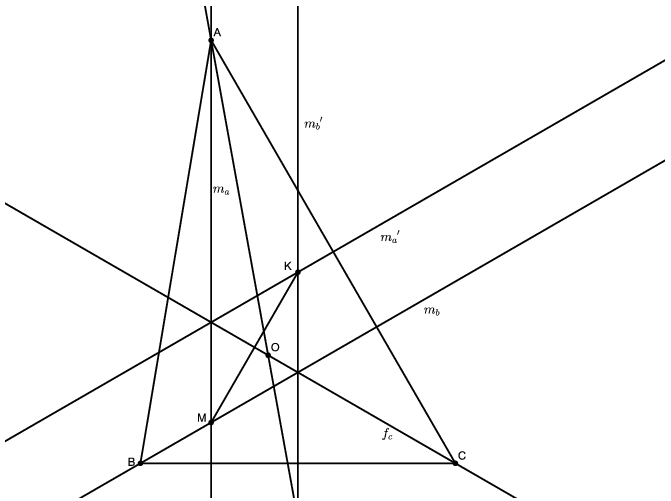
Megoldás. Belátjuk, hogy ha az \(\displaystyle ABC\) háromszög egyik szöge \(\displaystyle 60^{\circ}\)-os, de a háromszög nem szabályos, akkor az állítás teljesül. Legyen ez a szög a \(\displaystyle C\)-nél levő, és jelöljük az oldalakat és a magasságegyeneseket a szokásos módon. Ekkor \(\displaystyle m_a\) az \(\displaystyle a\) oldalt \(\displaystyle C\)-től \(\displaystyle b\cos60^{\circ}=\frac b2\) távolságban metszi. Hasonlóan \(\displaystyle m_b\) a \(\displaystyle b\) oldalt \(\displaystyle C\)-től \(\displaystyle a\cos60^{\circ} =\frac a2\) távolságban (lásd az ábrát). Ugyanakkor az \(\displaystyle a\) és a \(\displaystyle b\) oldal egyenese egymásnak az \(\displaystyle ABC\) háromszög \(\displaystyle C\)-ből kiinduló szögfelező egyenesére, \(\displaystyle f_c\)-re vett tükörképei. Így \(\displaystyle m_a\) tükörképe \(\displaystyle f_c\)-re a \(\displaystyle b\)-re \(\displaystyle C\)-től \(\displaystyle \frac{b}{2}\) távolságban állított merőleges, melyet jelöljön \(\displaystyle m_a'\). Hasonlóan \(\displaystyle m_b\) tükörképe \(\displaystyle f_c\)-re az \(\displaystyle a\)-ra \(\displaystyle C\)-től \(\displaystyle \frac a2\) távolságban állított merőleges, amit \(\displaystyle m_b'\)-vel jelölünk. Nyilván \(\displaystyle m_a'\) és \(\displaystyle m_b'\) a megfelelő oldalfelező merőlegesek. Tehát a magasságvonalak \(\displaystyle M\) metszéspontjának \(\displaystyle f_c\)-re vett tükörképe az oldalfelező merőlegesek metszéspontja, azaz a körülírt kör \(\displaystyle K\) középpontja. Így \(\displaystyle M\) és \(\displaystyle K\) felezőmerőlegese a szögfelező (a két pont nem esik egybe, hiszen akkor \(\displaystyle c=b\) is teljesülne, és a háromszög szabályos lenne). Tehát \(\displaystyle O\) illeszkedik erre a felező merőlegesre. \(\displaystyle O\) nem lehet \(\displaystyle MK\) felezőpontja, hiszen az a Feuerbach-kör középpontja, ami csak szabályos háromszögre esik egybe a beírt kör középpontjával. Ugyanis a Feuerbach-kör és a beírt kör érinti egymást (lásd pl. Füredi Zoltán: A Feuerbach-kör érinti az érintő köröket), így a középpontok egybeesése esetén a körök is egybeesnének. Ám a Feuerbach-körre ráesnek az oldalfelezőpontok, míg a beírt kör érintési pontjai csak szabályos háromszögre lehetnek mind oldalfelezőpontok, mivel csak ekkor lehet \(\displaystyle s - a = s -b = s - c\). Így az \(\displaystyle OKM\) háromszög egy nem elfajuló egyenlő szárú háromszög.

Ágoston Péter (Fazekas M. Főv. Gyak. Gimn., 12. évf.)

Statistics:

34 students sent a solution.
6 points:	Adorján Dániel, Ágoston Péter, Andi Gabriel Brojbeanu, Bereczki Zoltán, Cseh Kristóf, Di Giovanni Márk, Fekete Panna, Forrás Bence, Geng Máté, Győrfi-Bátori András, Kúsz Ágnes, Lajkó Kálmán, Maga Balázs, Nagy Kartal, Nagy-György Pál, Petrényi Márk, Porupsánszki István, Sal Kristóf, Sándor Krisztián, Schrettner Bálint, Simkó Irén, Török Tímea, Török Zsombor Áron, Williams Kada.
5 points:	Mócsy Miklós.
2 points:	2 students.
1 point:	1 student.
0 point:	6 students.

Problems in Mathematics of KöMaL, February 2014