A B. 4610. feladat (2014. február)

B. 4610. Legyen az ABC hegyesszögű háromszög köré írt körének középpontja K, beírt körének középpontja O, magasságpontja pedig M. Lehetnek-e az O, K és M pontok egy egyenlő szárú háromszög csúcsai?

(Kvant)

(6 pont)

A beküldési határidő 2014. március 10-én LEJÁRT.

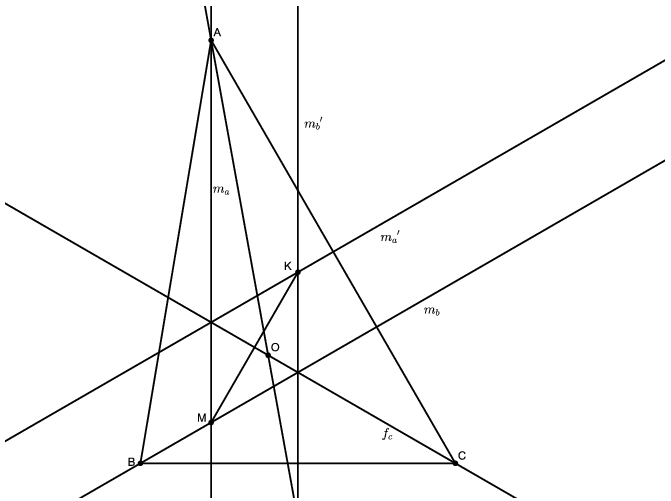
Megoldás. Belátjuk, hogy ha az \(\displaystyle ABC\) háromszög egyik szöge \(\displaystyle 60^{\circ}\)-os, de a háromszög nem szabályos, akkor az állítás teljesül. Legyen ez a szög a \(\displaystyle C\)-nél levő, és jelöljük az oldalakat és a magasságegyeneseket a szokásos módon. Ekkor \(\displaystyle m_a\) az \(\displaystyle a\) oldalt \(\displaystyle C\)-től \(\displaystyle b\cos60^{\circ}=\frac b2\) távolságban metszi. Hasonlóan \(\displaystyle m_b\) a \(\displaystyle b\) oldalt \(\displaystyle C\)-től \(\displaystyle a\cos60^{\circ} =\frac a2\) távolságban (lásd az ábrát). Ugyanakkor az \(\displaystyle a\) és a \(\displaystyle b\) oldal egyenese egymásnak az \(\displaystyle ABC\) háromszög \(\displaystyle C\)-ből kiinduló szögfelező egyenesére, \(\displaystyle f_c\)-re vett tükörképei. Így \(\displaystyle m_a\) tükörképe \(\displaystyle f_c\)-re a \(\displaystyle b\)-re \(\displaystyle C\)-től \(\displaystyle \frac{b}{2}\) távolságban állított merőleges, melyet jelöljön \(\displaystyle m_a'\). Hasonlóan \(\displaystyle m_b\) tükörképe \(\displaystyle f_c\)-re az \(\displaystyle a\)-ra \(\displaystyle C\)-től \(\displaystyle \frac a2\) távolságban állított merőleges, amit \(\displaystyle m_b'\)-vel jelölünk. Nyilván \(\displaystyle m_a'\) és \(\displaystyle m_b'\) a megfelelő oldalfelező merőlegesek. Tehát a magasságvonalak \(\displaystyle M\) metszéspontjának \(\displaystyle f_c\)-re vett tükörképe az oldalfelező merőlegesek metszéspontja, azaz a körülírt kör \(\displaystyle K\) középpontja. Így \(\displaystyle M\) és \(\displaystyle K\) felezőmerőlegese a szögfelező (a két pont nem esik egybe, hiszen akkor \(\displaystyle c=b\) is teljesülne, és a háromszög szabályos lenne). Tehát \(\displaystyle O\) illeszkedik erre a felező merőlegesre. \(\displaystyle O\) nem lehet \(\displaystyle MK\) felezőpontja, hiszen az a Feuerbach-kör középpontja, ami csak szabályos háromszögre esik egybe a beírt kör középpontjával. Ugyanis a Feuerbach-kör és a beírt kör érinti egymást (lásd pl. Füredi Zoltán: A Feuerbach-kör érinti az érintő köröket), így a középpontok egybeesése esetén a körök is egybeesnének. Ám a Feuerbach-körre ráesnek az oldalfelezőpontok, míg a beírt kör érintési pontjai csak szabályos háromszögre lehetnek mind oldalfelezőpontok, mivel csak ekkor lehet \(\displaystyle s - a = s -b = s - c\). Így az \(\displaystyle OKM\) háromszög egy nem elfajuló egyenlő szárú háromszög.

Ágoston Péter (Fazekas M. Főv. Gyak. Gimn., 12. évf.)

Statisztika:

34 dolgozat érkezett.
6 pontot kapott:	Adorján Dániel, Ágoston Péter, Andi Gabriel Brojbeanu, Bereczki Zoltán, Cseh Kristóf, Di Giovanni Márk, Fekete Panna, Forrás Bence, Geng Máté, Győrfi-Bátori András, Kúsz Ágnes, Lajkó Kálmán, Maga Balázs, Nagy Kartal, Nagy-György Pál, Petrényi Márk, Porupsánszki István, Sal Kristóf, Sándor Krisztián, Schrettner Bálint, Simkó Irén, Török Tímea, Török Zsombor Áron, Williams Kada.
5 pontot kapott:	Mócsy Miklós.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	6 versenyző.

A KöMaL 2014. februári matematika feladatai