Problem B. 4611. (February 2014)

B. 4611. Consider the composition of the reflections in the planes of all six faces of a cube in some order. How many different transformations of the spaces are obtained?

(6 pont)

Deadline expired on March 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Vegyünk fel egy térbeli derékszögű koordinátarendszert úgy, hogy az origója legyen a kocka egyik csúcsa, tengelyei essenek egybe a kocka e csúcsán átmenő élegyeneseivel, az egységet pedig válasszuk úgy, hogy a kocka origóval szemközti csúcsa az \(\displaystyle (1;1;1)\) pont legyen.

Ekkor a kocka lapsíkjainak egyenletei rendre \(\displaystyle X=0\), \(\displaystyle X=1\), \(\displaystyle Y=0\), \(\displaystyle Y=1\), \(\displaystyle Z=0\) és \(\displaystyle Z=1\) (1. ábra). Az e síkokra való tükrözések egy tetszőleges \(\displaystyle (a;b;c)\) pontot rendre a \(\displaystyle (-a;b;c)\), \(\displaystyle (2-a;b;c)\), \(\displaystyle (a;-b;c)\), \(\displaystyle (a;2-b;c)\), \(\displaystyle (a;b;-c)\) és \(\displaystyle (a;b;2-c)\) pontokba visznek át. Tehát a tükrözések során mindig csak a pont egyik koordinátája változik, párhuzamos síkokra való tükrözések esetén ugyanaz a koordináta, merőleges síkokra való tükrözések esetén pedig más-más koordináta. Vagyis az egymásra merőleges síkokra való tükrözések sorrendje felcserélhető, két egymással párhuzamos síkra való tükrözés pedig a pontok két-két koordinátáját változatlanul hagyja, egy koordinátáját pedig vagy 2-vel növeli, vagy 2-vel csökkenti (\(\displaystyle d\longmapsto -d \longmapsto 2-(-d)=d+2\), vagy \(\displaystyle d\longmapsto 2-d \longmapsto -(2-d)=d-2\), 2. ábra), azaz e két tükrözés egymásutánja egy olyan 2 hosszú vektorral való eltolás, mely vektor párhuzamos valamelyik koordinátatengellyel.

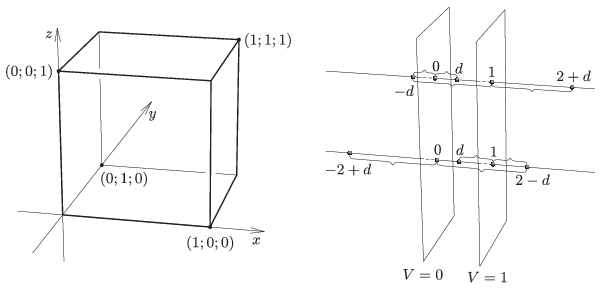
1. ábra                                                                   2. ábra

A hat tükrözés után tehát az \(\displaystyle (a;b;c)\) pont az \(\displaystyle (a\pm 2;b\pm 2;c\pm 2)\) pontba kerül. Vagyis a tükrözések egymásutánja megfelel egy eltolásnak valamely \(\displaystyle \mathbf{v}=(\pm 2;\pm 2;\pm 2)\) vektorral. Ezért az előjelek választásától (ami a párhuzamos síkokra való két-két tükrözés sorrendjén múlik) függően \(\displaystyle 2^3=8\) különböző transzformációt kaphatunk.

Olexó Gergely (Budapesti Fazekas M. Ált. Isk. és Gimn., 9. évf.) dolgozata alapján

Megjegyzés. A hat tükrözés egymásutánjaként kapott eltolások mindegyikének iránya párhuzamos a kocka valamelyik testátlójával, hossza pedig a testátló kétszerese.

Statistics:

82 students sent a solution.
6 points:	Ágoston Péter, Bereczki Ádám, Bereczki Zoltán, Csernák Tamás, Di Giovanni Márk, Fekete Panna, Fonyó Viktória, Forrás Bence, Győrfi-Bátori András, Gyulai-Nagy Szuzina, Horeftos Leon, Kabos Eszter, Kátay Tamás, Katona Dániel, Khayouti Sára, Kovács 246 Benedek, Kovács Balázs Marcell, Kúsz Ágnes, Leitereg Miklós, Maga Balázs, Nagy Gergely, Nagy Kartal, Nagy-György Pál, Olexó Gergely, Öreg Botond, Sándor Krisztián, Schwarcz Tamás, Simkó Irén, Szebellédi Márton, Szőke Tamás, Talyigás Gergely, Varga Rudolf, Williams Kada, Zsakó Ágnes.
5 points:	21 students.
4 points:	11 students.
3 points:	7 students.
2 points:	6 students.
1 point:	3 students.

Problems in Mathematics of KöMaL, February 2014