 Problem B. 4615. (March 2014)
Problem B. 4615. (March 2014)
B. 4615. Each angle of the triangle ABC is smaller than 120o. The isogonal point of the triangle is P. Draw lines through point P parallel to the sides. The parallels intersect side AB at D and E, side BC at F and G, and side CA at H and I. Let K, L and M denote the isogonal points of triangles DEP, FGP, HIP, respectively. Show that triangle KLM is equilateral.
Suggested by: Sz. Miklós, Herceghalom
(5 pont)
Deadline expired on April 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ismert, hogy az izogonális pont úgy is megszerkeszthető, hogy a háromszög oldalaira kifelé szabályos háromszögeket szerkesztünk, majd ezek külső csúcsait az eredeti háromszög ellentétes csúcsával összekötjük. A három összekötő szakasz egy pontban, a háromszög izogonális pontjában metszi egymást. Legyenek az \(\displaystyle AB\), \(\displaystyle BC\) és \(\displaystyle CA\) oldalakra kifelé rajzolt szabályos háromszögek harmadik csúcsai rendre \(\displaystyle U\), \(\displaystyle V\), \(\displaystyle Z\). Az is ismert, hogy a \(\displaystyle P\)-nél keletkező hat darab szög mindegyike \(\displaystyle 60^{\circ}\)-os.
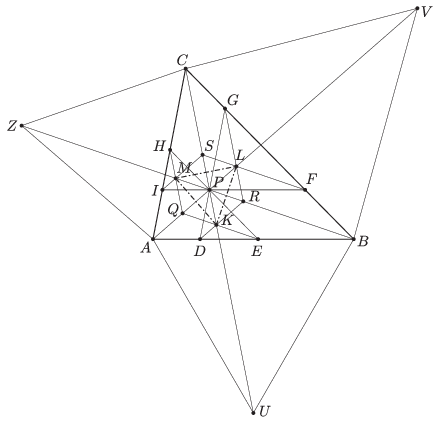
A \(\displaystyle CU\) egyenes egybeesik a \(\displaystyle PK\) egyenessel, hiszen a \(\displaystyle PDE\) háromszög minden oldala párhuzamos az \(\displaystyle ABC\) háromszög megfelelő oldalaival, tehát a csúcsokból az izogonális pontba menő egyenesek is párhuzamosak. Mivel ezek a két háromszög esetében átmennek a \(\displaystyle P\) ponton is, ezért egybeesnek. Ugyanezt beláthatjuk a \(\displaystyle GPF\) és \(\displaystyle HPI\) háromszögeknél is a megfelelő oldalakkal. Ugyanezzel a módszerrel azt is bizonyíthatjuk, hogy a \(\displaystyle HAE\), \(\displaystyle DBG\) és \(\displaystyle FCI\) háromszögek izogonális pontjai is rajta vannak a \(\displaystyle P\) pontot a megfelelő csúccsal összekötő szakaszokon. Legyenek ezek az izogonális pontok rendre \(\displaystyle Q\), \(\displaystyle R\) és \(\displaystyle S\). A \(\displaystyle KLM\) háromszög izogonális pontja \(\displaystyle P\), mert az eddigiek alapján \(\displaystyle MPK\sphericalangle=KPL\sphericalangle= LPM\sphericalangle= 120^{\circ}\). Most használjuk fel azt a fentebb már említett tulajdonságot, hogy az izogonális pontnál keletkező szögek mindegyike \(\displaystyle 60^{\circ}\). A \(\displaystyle K\), \(\displaystyle L\), \(\displaystyle M\), \(\displaystyle Q\), \(\displaystyle R\), \(\displaystyle S\) pontok mindegyike izogonális pont, tehát a \(\displaystyle PKR\), \(\displaystyle RPL\), \(\displaystyle LPS\), \(\displaystyle SPM\), \(\displaystyle MPQ\) és \(\displaystyle QPK\) háromszögek mindegyike szabályos, egymással egybevágó háromszög. A \(\displaystyle KPL\), \(\displaystyle LPM\) és \(\displaystyle LPM\) háromszögek \(\displaystyle 120^{\circ}\)-os szárszögű egyenlő szárú háromszögek, az alapon fekvő szögek \(\displaystyle 30^{\circ}\)-osak, a \(\displaystyle KLM\) háromszög tehát szabályos.
Kocsis Júlia (Dunakeszi, Radnóti Miklós Gimn., 9. évf.) dolgozata alapján
Statistics:
43 students sent a solution. 5 points: Adorján Dániel, Ágoston Péter, Andi Gabriel Brojbeanu, Baran Zsuzsanna, Bereczki Zoltán, Bodolai Előd, Cseh Kristóf, Csépai András, Demeter Dániel, Di Giovanni Márk, Fekete Panna, Forrás Bence, Geng Máté, Győrfi-Bátori András, Gyulai-Nagy Szuzina, Jenei Dániel Gábor, Kacz Dániel, Katona Dániel, Kocsis Júlia, Kovács 972 Márton, Kúsz Ágnes, Lajkó Kálmán, Maga Balázs, Mócsy Miklós, Nagy Gergely, Nagy-György Pál, Porupsánszki István, Sándor Krisztián, Schrettner Bálint, Schwarcz Tamás, Simkó Irén, Stein Ármin, Szebellédi Márton, Williams Kada. 4 points: Bősze Zsófia, Sal Kristóf, Torma Bence, Zarándy Álmos. 3 points: 1 student. 2 points: 3 students. 1 point: 1 student.
Problems in Mathematics of KöMaL, March 2014
