Problem B. 4617. (March 2014)

B. 4617. What angle may the hypotenuse of a right-angled triangle enclose with the median drawn to one of the legs?

Javasolta: G. Holló, Budapest

(4 pont)

Deadline expired on April 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen az \(\displaystyle ABC\) derékszögű háromszög \(\displaystyle AB\) átfogójának felezőpontja \(\displaystyle E\), \(\displaystyle BC\) befogójának felezőpontja \(\displaystyle F\), a befogóhoz tartozó súlyvonalnak és az \(\displaystyle AB\) átfogónak a szöge \(\displaystyle \alpha\), az \(\displaystyle AB\) átfogó Thalész-köre \(\displaystyle k\), ennek a \(\displaystyle B\) középpontú, 1/2 arányú középpontos hasonlóságnál kapott képe pedig az \(\displaystyle m\) kör. Ekkor \(\displaystyle m\) az \(\displaystyle EB\) szakasz Thalész-köre, középpontja az \(\displaystyle AB\) szakasz \(\displaystyle B\)-hez legközelebbi \(\displaystyle O\) negyedelőpontja (1. ábra).

Az \(\displaystyle F\) pont felezi \(\displaystyle BC\)-t és \(\displaystyle C\) rajta van \(\displaystyle k\)-n, ezért \(\displaystyle F\) rajta van \(\displaystyle m\)-en, tehát az \(\displaystyle AF\) egyenesnek és \(\displaystyle m\)-nek van közös pontja. Így \(\displaystyle \alpha\) legfeljebb akkora, mint az \(\displaystyle A\)-ból \(\displaystyle m\)-hez húzott \(\displaystyle AD\) érintő és \(\displaystyle AB\) által bezárt \(\displaystyle \beta\) szög. Ezt a szöget az \(\displaystyle AOD\) derékszögű háromszögből határozhatjuk meg.

\(\displaystyle \sin \beta =\frac{OD}{OA}=\frac{\frac{1}{4}AB}{\frac{3}{4}AB}=\frac{1}{3}, \quad \text{azaz} \quad \beta=\arcsin \frac{1}{3}\approx 19{,}47^{\circ}. \)

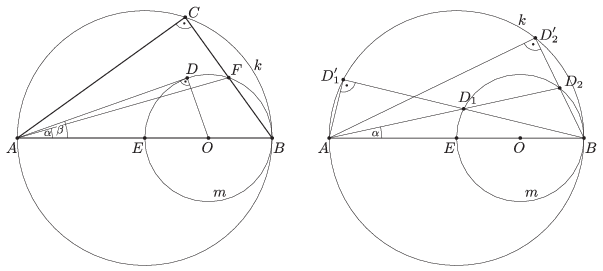
1. ábra                                                                       2. ábra

Megmutatjuk, hogy minden \(\displaystyle 0^{\circ} < \alpha \le \arcsin \frac{1}{3}\) esetén van olyan derékszögű háromszög, melyben az átfogó és az egyik befogóhoz tartozó súlyvonal szöge \(\displaystyle \alpha\). Ha a feltétel teljesül, akkor az \(\displaystyle AB\) egyenes egyik oldalára felmérve az \(\displaystyle \alpha \) szöget, annak \(\displaystyle AB\)-tól különböző szára metszi \(\displaystyle m\)-et a \(\displaystyle D_1\) és \(\displaystyle D_2\) pontokban, illetve érinti \(\displaystyle m\)-et \(\displaystyle D\)-ben, ha \(\displaystyle \alpha = \arcsin \frac{1}{3}\) (2. ábra). Mivel \(\displaystyle D_i\) rajta van \(\displaystyle m\)-en, azért ha \(\displaystyle B\)-ből kétszeresére nagyítjuk, akkor a kapott \(\displaystyle D_i'\) pont rajta lesz \(\displaystyle m\) kétszeresre nagyított képén, \(\displaystyle k\)-n, azaz az \(\displaystyle AB\) szakasz Thalész-körén. Ezért ha \(\displaystyle i=1,2\), akkor az \(\displaystyle ABD_i'\) háromszög derékszögű, és a \(\displaystyle BD'_i\) befogójához tartozó \(\displaystyle AD_i\) súlyvonala \(\displaystyle \alpha\) szöget zár be az átfogójával.

Scheidler Barnabás (Bonyhád, Petőfi S. Ev. Gimn., 8. évf.) dolgozatát felhasználva

Statistics:

104 students sent a solution.
4 points:	63 students.
3 points:	15 students.
2 points:	9 students.
1 point:	12 students.
0 point:	5 students.

Problems in Mathematics of KöMaL, March 2014