Problem B. 4623. (April 2014)

B. 4623. In a convex quadrilateral, the diagonals form four triangles of integer areas. Prove that the product of the four integers cannot end in 2014.

(3 pont)

Deadline expired on May 12, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Először megmutatjuk, hogy a két-két szemközti háromszög területének szorzata egyenlő. Jelölje a hároszögek területét az ábra szerint \(\displaystyle T_1\), \(\displaystyle T_2\), \(\displaystyle T_3\) és \(\displaystyle T_4\). A háromszögeknek az egyik átlóhoz tartozó magasságai legyenek \(\displaystyle m_1\) és \(\displaystyle m_2\), ennek az átlónak az átlók metszéspontja által meghatározott szakaszai pedig legyenek \(\displaystyle e_1\) és \(\displaystyle e_2\).

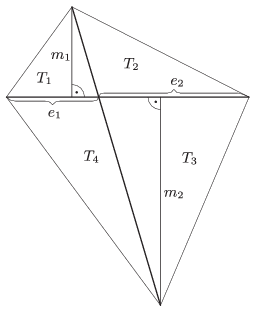
Ekkor

\(\displaystyle 2\,T_1=e_1m_1, \quad 2\,T_2=e_2m_1, \)

\(\displaystyle 2\,T_3=e_2m_2 \quad \text{és} \quad 2\,T_4=e_1m_2,\)

tehát

\(\displaystyle T_1T_3=\frac{e_1e_2m_1m_2}{4}=T_2T_4. \)

Ezért \(\displaystyle T_1T_2T_3T_4= {(T_1T_3)}^2\), vagyis a négy terület szorzata négyzetszám. Tudjuk, hogy a négyzetszámok 4-gyel osztva \(\displaystyle 0\) vagy \(\displaystyle 1\) maradékot adnak. Mivel a számok 4-es maradéka csak az utolsó két számjegyüktől függ, ezért ha egy szám \(\displaystyle 2014\)-re végződik, akkor a 4-es maradéka megegyezik a \(\displaystyle 14\)-nek a 4-es maradékával, azaz 2-vel. Tehát a területek szorzata nem végződhet \(\displaystyle 2014\)-re.

Varga Péter (Hajdúszoboszló, Hőgyes E. Gimn. és Szki., 10. évf.) dolgozata alapján

Statistics:

125 students sent a solution.
3 points:	105 students.
2 points:	7 students.
1 point:	8 students.
0 point:	4 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, April 2014