 Problem B. 4624. (April 2014)
Problem B. 4624. (April 2014)
B. 4624. In a trapezium \(\displaystyle ABCD\), let \(\displaystyle E\) and \(\displaystyle F\) denote the midpoints of the bases \(\displaystyle AB\) and \(\displaystyle CD\), respectively, and let \(\displaystyle O\) denote the intersection of the diagonals. A line parallel to the bases intersects the line segments \(\displaystyle OA\), \(\displaystyle OE\) and \(\displaystyle OB\) at points \(\displaystyle M\), \(\displaystyle N\) and \(\displaystyle P\), respectively. Show that the quadrilaterals \(\displaystyle APCN\) and \(\displaystyle BNDM\) have equal areas.
Suggested by L. Longáver, Nagybánya
(3 pont)
Deadline expired on May 12, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A négyszögeket az \(\displaystyle MN\), illetve \(\displaystyle NP\) átlók két-két háromszögre bontják, ezért
\(\displaystyle T_{APCN} =T_{APN}+T_{PCN} \quad\text{és}\)
\(\displaystyle T_{BNDM} =T_{BNM}+T_{NDM}.\)
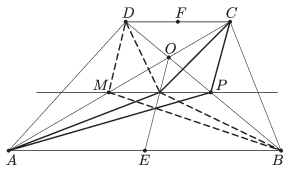
Az \(\displaystyle MNP\) egyenes párhuzamos a trapéz alapjaival. Ebből egyrészt a párhuzamos szelőszakaszok tétele alapján
\(\displaystyle \frac{MN}{AE}=\frac{NP}{EB}, \quad \text{vagyis} \quad \frac{MN}{NP}=\frac{AE}{EB} \)
következik, s mivel \(\displaystyle E\) felezi az \(\displaystyle AB\) szakaszt, ezért kapjuk, hogy \(\displaystyle MN=NP\). Másrészt a párhuzamosság miatt a \(\displaystyle PCN\) és \(\displaystyle NDM\) háromszögek \(\displaystyle C\) illetve \(\displaystyle D\), valamint az \(\displaystyle APN\) és \(\displaystyle BNM\) háromszögek \(\displaystyle A\), illetve \(\displaystyle B\) csúcsaihoz tartozó magasságok is megegyeznek. Ezért
\(\displaystyle T_{APN}=T_{BNM} \quad \text{és} \quad T_{PCN}=T_{NDM}, \)
amiből a feladat állítása következik.
Nagy Odett (Szeged, Radnóti M. Gimn., 9. évf.) dolgozata alapján
Statistics:
128 students sent a solution. 3 points: 111 students. 2 points: 9 students. 1 point: 4 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, April 2014
