 Problem B. 4627. (April 2014)
Problem B. 4627. (April 2014)
B. 4627. The angle bisector drawn from right-angled vertex \(\displaystyle C\) of triangle \(\displaystyle ABC\) intersects the circumscribed circle at point \(\displaystyle P\), and the angle bisector from vertex \(\displaystyle A\) intersects the circumscribed circle at point \(\displaystyle Q\). \(\displaystyle K\) is the intersection of line segments \(\displaystyle PQ\) and \(\displaystyle AB\). The centre of the inscribed circle is \(\displaystyle O\), and its point of tangency on side \(\displaystyle AC\) is \(\displaystyle E\). Prove that points \(\displaystyle E\), \(\displaystyle O\) and \(\displaystyle K\) are collinear.
Suggested by Zs. Sárosdi, Veresegyház
(4 pont)
Deadline expired on May 12, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen \(\displaystyle CAB\sphericalangle =\alpha\), ekkor \(\displaystyle CBA\sphericalangle =\beta=90^{\circ}-\alpha\). A kerületi szögek tétele miatt:
\(\displaystyle CPA\sphericalangle =CBA\sphericalangle =90^{\circ}-\alpha, \)
hasonlóan
\(\displaystyle BAQ\sphericalangle =CAQ\sphericalangle =CPQ\sphericalangle =\frac{\alpha}{2}. \)
Így \(\displaystyle OAK\sphericalangle =OPK =\frac{\alpha}{2}\), ezért \(\displaystyle OKPA\) húrnégyszög. Az \(\displaystyle OKPA\) húrnégyszög köré írt körben \(\displaystyle OKA\sphericalangle =OPA\sphericalangle =90^{\circ}-\alpha\), mivel azonos íven nyugvó kerületi szögek.
Hosszabbítsuk meg \(\displaystyle OK\)-t, legyen \(\displaystyle OK\) és \(\displaystyle AC\) metszéspontja \(\displaystyle D\). A háromszög belső szögeinek összege \(\displaystyle 180^{\circ}\), ezért
\(\displaystyle KDA\sphericalangle =180^{\circ}-DKA\sphericalangle -DAK\sphericalangle =90^{\circ}. \)
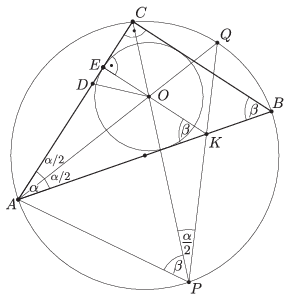
Így \(\displaystyle KDA\sphericalangle =90^{\circ}\). Az \(\displaystyle O\)-nak az \(\displaystyle AC\)-re való merőleges vetülete az \(\displaystyle E\) pont. Ebből következik, hogy \(\displaystyle D=E\), tehát \(\displaystyle E\), \(\displaystyle O\) és \(\displaystyle K\) kollineárisak.
Szebellédi Márton (Budapesti Fazekas M. Ált. Isk. és Gimn., 10. évf.) dolgozata alapján
Statistics:
68 students sent a solution. 4 points: 57 students. 3 points: 4 students. 2 points: 3 students. 1 point: 4 students.
Problems in Mathematics of KöMaL, April 2014
