 Problem B. 4632. (May 2014)
Problem B. 4632. (May 2014)
B. 4632. The intersection of two given lines is off the page. Consider the line that passes through a given point on the page and through the intersection of the given lines. Of this line, construct the part on the page.
(3 pont)
Deadline expired on June 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az adott egyenes és a lap szélének a metszéspontjai legyenek \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\), a két egyenes metszéspontja \(\displaystyle M\), az adott pont pedig \(\displaystyle P\).
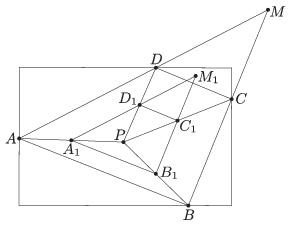
Alkalmazzunk az \(\displaystyle ABCD\) négyszögre egy \(\displaystyle P\) középpontú, \(\displaystyle \frac{1}{2}\) arányú kicsinyítést. Ezt könnyen megtehetjük, hiszen az \(\displaystyle AP\), \(\displaystyle BP\), \(\displaystyle CP\) és \(\displaystyle DP\) szakaszok \(\displaystyle A_{1}\), \(\displaystyle B_{1}\), \(\displaystyle C_{1}\) és \(\displaystyle D_{1}\) felezőpontjai a papírra esnek. Az \(\displaystyle A_{1}D_{1}\) és \(\displaystyle B_{1}C_{1}\) egyenesek metszéspontja adja az \(\displaystyle M\) pont képét, \(\displaystyle M_{1}\)-et, és \(\displaystyle P\), \(\displaystyle M_{1}\) és \(\displaystyle M\) egy egyenesen vannak. Tehát, ha az \(\displaystyle M_{1}\) pont a papírra esik, akkor a \(\displaystyle PM_{1}=PM\) egyenes megszerkeszthető. Ha \(\displaystyle M_{1}\) még nem esik a papírra, akkor folytathatjuk az eljárást az \(\displaystyle A_{1}B_{1}C_{1}D_{1}\) négyszög \(\displaystyle P\) pontra vonatkozó, \(\displaystyle \frac{1}{2}\) arányú kicsinyítésével. Ha a keletkező \(\displaystyle M_{2}\) pont sem esik a papírra, akkor az eljárást mindaddig folytatjuk, amíg az \(\displaystyle M_{n}\) pont már a papírra fog esni. Ez véges lépésben elérhető. A keresett egyenes a \(\displaystyle PM_{n}\) lesz.
Győrfy-Bátori András (Kaposvári Táncsics Mihály Gimn., 12. évf.) dolgozata alapján
Statistics:
89 students sent a solution. 3 points: Baran Zsuzsanna, Csernák Tamás, Csilling Tamás, Di Giovanni Márk, Fonyó Viktória, Győrfi-Bátori András, Hansel Soma, Janzer Orsolya Lili, Katona Dániel, Kovács 972 Márton, Mándoki Sára, Nagy Kartal, Nagy-György Pál, Radnai Bálint, Schwarcz Tamás, Szebellédi Márton, Tóth Viktor, Vágó Ákos, Vu Mai Phuong, Williams Kada. 2 points: 41 students. 1 point: 24 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, May 2014
