A B. 4670. feladat (2014. december)

B. 4670. Az \(\displaystyle ABC\) háromszög oldalainak felezőpontjai legyenek \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\). Bocsássunk \(\displaystyle A_1\)-ből merőlegest az \(\displaystyle A\) csúcshoz tartozó szögfelezőre, \(\displaystyle B_1\)-ből a \(\displaystyle B\)-hez, \(\displaystyle C_1\)-ből pedig a \(\displaystyle C\)-hez tartozóra. A \(\displaystyle B_1\)-et tartalmazó merőleges és a \(\displaystyle C_1\)-et tartalmazó merőleges metszéspontja legyen \(\displaystyle A_2\), hasonlóan kapjuk a \(\displaystyle B_2\), \(\displaystyle C_2\) pontokat. Mutassuk meg, hogy az \(\displaystyle A_1A_2\), \(\displaystyle B_1B_2\), \(\displaystyle C_1C_2\) egyenesek egy pontban metszik egymást.

Javasolta: Sárosdi Zsombor (Veresegyház)

(3 pont)

A beküldési határidő 2015. január 12-én LEJÁRT.

Megoldási ötlet: Tekintsük az \(\displaystyle A_1B_1C_1\) háromszög szögfelezőit.

Megoldás. Legyenek az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) pontokból induló belső szögfelezők \(\displaystyle f_{a}\), \(\displaystyle f_{b}\), \(\displaystyle f_{c}\). Az \(\displaystyle A_{1}B_{1}C_{1}\) középvonal háromszög belső szögfelezői legyenek \(\displaystyle f_{a_{1}}\), \(\displaystyle f_{b_{1}}\), \(\displaystyle f_{c_{1}}\). Az \(\displaystyle ABC\) és \(\displaystyle A_{1}B_{1}C_{1}\) háromszögek oldalai páronként párhuzamosak és megfelelő szögeik egyenlők, ezért \(\displaystyle f_{a_{1}}\parallel f_{a}\), \(\displaystyle f_{b_{1}}\parallel f_{b}\), \(\displaystyle f_{c_{1}}\parallel f_{c}\).

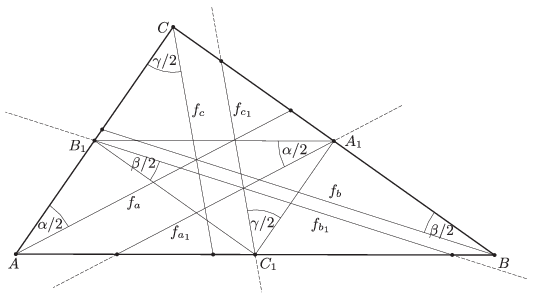
Ezért az \(\displaystyle A_{1}\), \(\displaystyle B_{1}\), \(\displaystyle C_{1}\) pontokból az \(\displaystyle f_{a}\), \(\displaystyle f_{b}\), \(\displaystyle f_{c}\) szögfelezőkre bocsájtott merőlegesek az \(\displaystyle f_{a_{1}}\), \(\displaystyle f_{b_{1}}\), \(\displaystyle f_{c_{1}}\) egyenesekre is merőlegesek lesznek, és így ezek lesznek az \(\displaystyle A_{1}B_{1}C_{1}\triangle\) külső szögfelezői.

Egy háromszög két csúcsában húzott külső és a harmadik csúcsban húzott belső szögfelezője egy pontban, a háromszög hozzáírt körének középpontjában metszi egymást, ezért az \(\displaystyle A_{1}B_{1}C_{1}\triangle\) külső szögfelezőinek \(\displaystyle A_{2}\), \(\displaystyle B_{2}\), \(\displaystyle C_{2}\) metszéspontjain rendre áthaladnak az \(\displaystyle f_{a_{1}}\), \(\displaystyle f_{b_{1}}\), \(\displaystyle f_{c_{1}}\) szögfelezők. Ezek rendre egybeesnek az \(\displaystyle A_{1}A_{2}\), \(\displaystyle B_{1}B_{2}\), \(\displaystyle C_{1}C_{2}\) egyenesekkel.

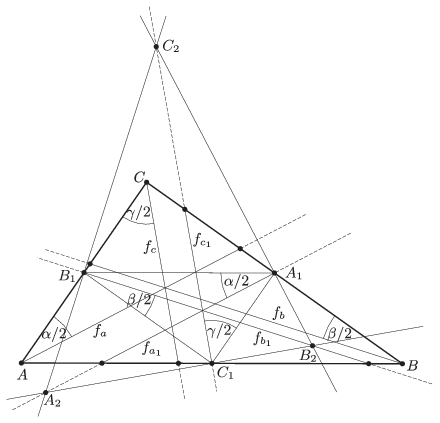
Vagyis az \(\displaystyle A_{1}A_{2}\), \(\displaystyle B_{1}B_{2}\), \(\displaystyle C_{1}C_{2}\) egyenesek az \(\displaystyle A_{1}B_{1}C_{1}\triangle\) belső szögfelezői, ezért egy pontban metszik egymást.

Gál Boglárka (Veszprém, Lovassy L. Gimn. 12. évf.) dolgozata alapján

Statisztika:

36 dolgozat érkezett.
3 pontot kapott:	Csépai András, Gál Boglárka, Geng Máté, Gyulai-Nagy Szuzina, Heinc Emília, Juhász 326 Dániel, Kerekes Anna, Khayouti Sára, Nagy Dávid Paszkál, Németh 123 Balázs, Polgár Márton, Vankó Miléna, Várkonyi Dorka, Williams Kada.
2 pontot kapott:	Andó Angelika, Ratkovics Gábor, Sal Kristóf, Szakály Marcell, Szász Dániel Soma.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	9 versenyző.

A KöMaL 2014. decemberi matematika feladatai